“Why is surprise the permanent condition of the political and economic elite?”

The above (somewhat abbreviated) question is how Nassim Taleb and author Mark Blyth open their essay The Black Swan of Cairo, published in the May/June issue of Foreign Affairs in 2011. The essay takes note of the then-recent turmoil in Egypt, Tunisia and Libya (now know as “the Arab spring”),where suddenly and seemingly out of nowhere, highly suppressive political regimes came tumbling down. The essay describes the 2011 events as prototypical examples of what happens when complex systems that have been artificially suppressing volatility “become fragile, while at the same time exhibiting no visible risks”. Taleb in particular made his career by describing such “black swan” events, which quote, “come as a surprise”, “have a major effect”, and “are often inappropriately rationalized after the fact with the benefit of hindsight” (Taleb and Blyth, 2011).

How exactly should we be thinking about black swan events — mathematically? Are they tail risks? Those highly improbable, unlikely potential events that fall outside of every VaR model due to their improbability? Or are they statistical inevitabilities, unresponsive to regulatory efforts and strategic manipulation? Are Taleb and Blyth right in their assertion that in “artificially suppressing” tail risks, “the longer it takes for the blowup to occur, the worse the resulting harm”? What about the relationship between the probability of a black swan and the effects of their outcome?

What really defines a black swan event? Read on.

Black Swan Events

“No amount of observations of white swans can allow the inference that all swans are white, but the observation of a single black swan is sufficient to refute that conclusion.” — John Stuart Mill

The metaphoric black swan is described by Wikipedia as an “event that comes as a surprise, has a major effect and is often inappropriately rationalized after the fact with the benefit of hindsight”. The term itself has its origin from the 2nd-century roman poet Juvenal and his characterization of something being rara avis in terris nigroque simillima cygno (“a rare bird in the lands and very much like a black swan”). Black swans were, both at the time and for the next 1300 years, indeed thought by Europeans not to exist. This presumption was disconfirmed by Dutch explorers lead by Willem de Vlamingh who in 1697 indeed discovered black swans (“Cygnus atratus”) in Western Australia.

Since then, most prominently, Nassim Nicholas Taleb has made use of the metaphor in his book Fooled by Randomness (2001) and its follow-up The Black Swan (2007). Here black swans are used as a vehicle for discussing the human propensity to underestimate the degree to which randomness factors into every day life. Taleb applies the following three criteria to identify what he defines as “black swan events”:

"First, it is an outlier, as it lies outside the realm of regular expectations, because nothing in the past can convincingly point to its possibility. Second, it carries an extreme 'impact'. Third, in spite of its outlier status, human nature makes us concoct explanations for its occurrence after the fact, making it explainable and predictable"- Excerpt, "The Black Swan" by Nassim Nicholas Taleb (2007)

<sidenote>

To the best of my knowledge Taleb has never quite come to describe exactly how the second criteria, “extreme impact”, fits into the black swan metaphor. What exactly was the extreme consequence of discovering a black swan (the bird) ?

</sidenote>

Predicting Future Events

I do like the distinction Taleb and Blyth’s make in their Foreign Affairs article between the two types of domains humans inhabit, the linear and complex, and their accompanying characteristics:

• The linear domain: predictable with low degree of interaction between components/factors, enabling the use of mathematical methods that make forecasts reliable; and
• The complex domain: an absence of causal links between the elements masking a high degree of interdependence and extremely low predictability;

Engineering, astronomy and most of physics and biology are prototypical linear domains. They are those fields in which we can reliably model phenomena mathematically and empirical observations behave according to the predictions of our models. They are the domains which in some sense operate the same regardless of human behavior, where assumptions of rationality and perfect information are not necessary for models to work — in fact, where such assumptions would introduce noise rather than strengthen predictions.

Economics, epidemiology, nutrition science, quantum physics and psychology are not linear domains. Common to them, rather, are highly non-linear, even seemingly random factors that arise either due to causes we simply don’t understand (e.g. quantum physics) or, causes which have such high degrees of interdependence that ex ante predictions are computationally unattainable (“simply too many variables”). Rather, predictions become available only ex post.As Taleb and Blyth write, “human nature makes us concoct explanations for occurrences after the fact, making them explainable and predictable”. Although they should not be confused with indiscernible systems, rather, complex systems are perhaps best described as ex ante computationally inaccessible systems — systems in which predictions are uncomputable, either from a lack of information about causality (as in the case of quantum theory), or an abundance of information (such as in social science).

To illustrate the difference, let us review a handful of scenarios and attempt to classify them as either as linear or complex systems, and review whether their assumptions adhere to something describable as a black swan, according to Taleb’s three criteria above.

Malthusian Catastrophe

Included for its historical relevance, one of the prototypical global catastrophe risks is the theoretical Malthusian catastrophe. Thomas Robert Malthus (1766–1834) was an English academic and demographer who rose to prominence with his 1798 publication An Essay on the Principle of Population. The book is most well known for its main claim that because population multiplies geometrically while food cumulates arithmetically, whenever the food supply increases, populations will rapidly grow to eliminate the abundance. In other words, given these two growth rate assumptions and their implication that food supply is both the enabling and limiting factor of population growth, at some point there will not be enough food for humanity to consume and people will starve, leading to a rapid, population crash.

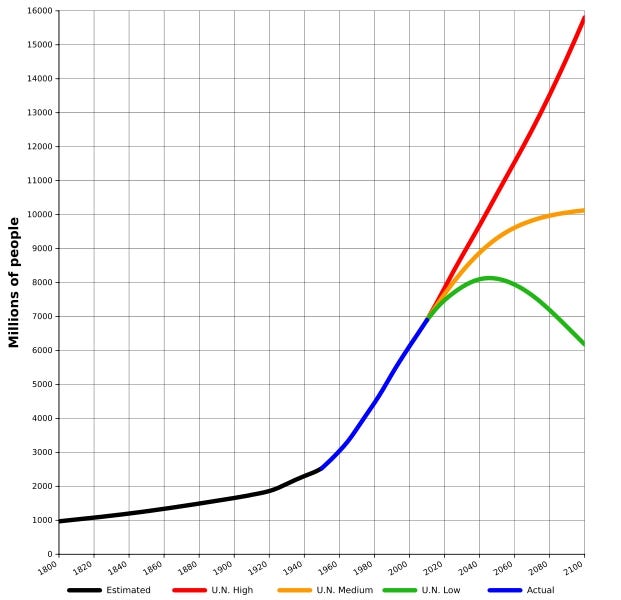
In the chart above, the green estimate by the U.N represents a “Malthusian catastrophe” in that population growth has outpaced agricultural production and starvation leads to rapid population decline. One might argue that humanity is indeed heading for such a Malthusian catastrophe as you read this article. A UN study conducted in 2009 for instance said that as a result of an increasing population, food production will have to increase by 70% over the next 40 years to keep up. So let us review: would a “Malthusian catastrophe” be considered a black swan?

Let’s evaluate the second criterion first, since it is the most easily confirmed/dispelled:

• Does it carry an extreme impact?

Yes indeed, rapid population crash would be extreme.

• Does it lay outside the realm of regular expectations?

Meaning something which would strike the vast majority of humanity as highly unexpected? Indeed. Meaning something that has never been imagined before? Not quite. After all, Malthus wrote about it in 1798 and I am indeed still writing about it in 2019. Then..?

• Does it lay outside the realm of regular expectations because nothing in the past can convincingly point to its possibility?

This I find harder to discern. Humanity certainly experiences famines from time to time, both as the result of war, inflation, crop failure, government policies and, indeed, population imbalance. Overall though, both the global population and food supply have steadfastly been on the rise. Some countries (most notably now many ex-Soviet states and Japan) are indeed currently in population decline, as those born during their peak-level of birth rates begin to pass on and those who are young emigrate to find better opportunities. However, neither can really be said to be in population decline as a function of food supply. As such, it would indeed be unexpected if the world faced a rapid population crash for this reason specifically.

Two for two, I’d say. Finally:

• In spite of its outlier status, would explanations for its occurrence after the fact, make it explainable and predictable?

That would depend on the cause, and this is where we arrive at the root of my argument. Namely, that black swan events seem less so to be sufficiently defined according to their properties of either low probability of occurrence or scope of impact, but rather, why they occur at all.

Peak oil

To highlight what I mean, let’s investigate another supposed global catastrophe risk, peak oil. Peak oil is the theorised point in time in which the maximum rate of extraction of petroleum is reached. The idea was first formalized by geologist M. King Hubbert in his 1956 paper Nuclear Energy and the Fossil Fuels proposing what has since become known as the Hubbert peak theory:

“For any given geographical area, from an individual oil-producing region to the planet as a whole the rate of petroleum production tends to follow a bell-shaped curve.”

Up until 1956, the cumulative production of oil had been 90 billion barrels, and Hubbert’s prediction was that we would reach peak production around the year 2000 of about 12.5 billion barrels per year. As of 2016, the world’s oil production was 29.4 billion barrels per year, with seemingly no signs of slowdown in production in sight (assuming a certain price elasticity of demand). Predicted consequences of reaching peak oil have ranged from the catastrophic to the rather minor. Most generally, peak oil is predicted to lead to a negative global economy and a subsequent oil price increase due to the dependence of most modern and developing industrial nations on low cost and high availability of oil. Would we consider this a black swan event?

• Does it carry an extreme impact?

Before we answer this question in the affirmative, in this case, it is prudent to introduce the variable of the technological environment as an additional enabling and/or limiting factor. Say, if we for instance discovered that somehow measurements of oil production over the last ten years had been off, and peak oil had actually occurred in 2009, then yes indeed, one might argue that the occurrence of peak oil could lead to a run-off in prices and a resulting extreme impact, especially in the developing world (“there isn’t as much oil left as we thought, let’s buy as much as possible immediately”). However, barring such hypotheticals, if it were to happen today, by its nature and the technological environment we live in, there would be ample time for regulators, companies and individuals to adjust to more sustainable fuel sources. After all, another term for peak oil might just be “half of all proven reservoirs are extracted”. In such a more probable scenario, no, the impact might not be extreme — given the benefits of both ample time and technology.

Water scarcity

Our third and final potential existential black swan event is a lack of drinkable fresh water, which in 2019 was listed by the World Economic Forum as one of the largest global risks in terms of potential impact over the next decade. Water, like oil, is indeed a finite resource, albeit one that (unlike oil) circulates through the hydrological cycle, and so does not get “used up”. However, given:

1. Only 0.014% of the world’s water is both fresh and easily accessible;
2. The world’s population is increasing, and hence, demand for fresh water is growing; and
3. Unequal distribution of fresh water leads to some very wet and some very dry geographic locations

One might indeed argue that we are heading towards a crisis if water, like oil, becomes a scarce resource globally due to a rapid increase in demand (e.g. as the result of a rapidly increasing population) or, a rapid decrease in supply (e.g. from a disruption of the hydrological cycle due to climate change). Would it be a black swan?

• In spite of its outlier status, would explanations for its occurrence after the fact make it explainable and predictable?

Here again I come back to my main argument, about causality. If nothing else changes except a growing population, leading to water scarcity, then no, I don’t think we should consider it a black swan, as we’re currently discussing it as a possibility. Although it is an outlier somewhere in the far tail of the bell curve of possible futures, it is still within our view.

However, if something like a meteor or climate change altered the hydrological cycle such that all the world’s fresh water somehow became inaccessible, extremely difficult to extract, or some other outcome which I cannot imagine let alone describe — now we’re in the realm of the complex, the unexpected, the risks way beyond our purview — this to me sounds more like a black swan.

Complexity

Thus, as only our final example above could really qualify as a potential black swan, let us evaluate its crucial difference from the other examples discussed. In my opinion, it is the introduction of a complex factor (e.g. meteor impact, climate change, etc), something of which we completely lack predictive power, and thus satisfies the following condition:

Condition for a Black Swan Event For an event to be classified as a black swan event, it must be ex ante computationally inaccessible

Now, that isn’t to say that we can’t build models that generate useful predictions about the effects of climate change on water scarcity. Rather, what it implies is that those models will have to be based on probabilities, not tangible causal links. Determinism cannot be assumed (see quantum theory vs. classical physics). Causality gets fuzzy, politics get complicated.

As Taleb points out again and again, humans are generally uncomfortable with nondeterminism. Even when we know a system is best defined by probabilities, we tend to search for deterministic explanations of why something complex “is actually, in this case..” linear. From a post I found on Quora:

"Here’s a poker analogy: in Texas hold ‘em the longest odds are when you have exactly one opponent left and they must catch perfect [cards] twice, with perfect consisting of 1 of 2 cards on the turn, and exactly 1 of 1 card on the last card, or River. The odds are approximately 988–1 of [it] occurring.So, when it does happen, especially if during an “on line” game, the lesser informed will “see” a hoax being perpetrated. Especially if they were the ones facing that 988–1 shot."- Shawn Nelsen, Professional Poker Player

There are, after all, whole cities in Las Vegas, Macau, Monte Carlo and Atlantic City financed by the lacking human ability to accept complexity and probability, for the safe haven of linearity.