You may have heard of this incredibly large number called Graham’s number, but more often than not when this subject is discussed, Graham’s number is rarely given in context. What does it mean? Did mathematicians decide to write down a really big number one Sunday afternoon because they were bored?

No.

In fact, Graham’s number is related to a very elegant field of mathematics called Ramsey theory. I will give you a beginner’s guide to Ramsey theory before diving into the deep end with Graham’s Number.

Theorem

Suppose you are at a party. How many people need to be present such that you are guaranteed that at least three of them are (pairwise) mutual strangers or at least three of them are (pairwise) mutual friends?

I claim that the answer is six.

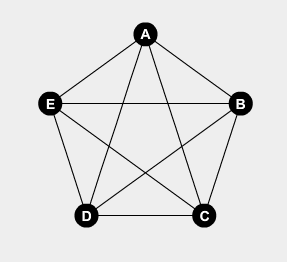
To prove this, we first turn this into a graph theory problem. We reduce each person attending to a point (formally known as a vertex) and draw lines (edges) between all the attendees. Below is an example of a party of five people:

This is known as a complete graph on 5 vertices (denoted K_5). Next step is we colour an edge red to denote that the two people it connects are strangers and blue if they are friends.

A specific case of such an arrangement is known as an edge colouring.

If three people mutually know each other (or don’t know each other resp.) then we are looking for a triangle of edges that are all the same colour.

Here we see that the people A, B, E form a red triangle and so are all mutual strangers. Similarly, C, D, E form a blue triangle and so all know each other.

This triangle is known as a 3-clique (3 because there are 3 vertices)and more generally is a subset of a graph where each vertex is connected to each other.

The problem can now fully be restated into a mathematical one:

What is the smallest integer N such that the complete graph K_N is guaranteed to either have a red 3-clique or blue 3-clique?

To answer, firstly we must show that 5 vertices (people) are insufficient. This is easily done by counter example:

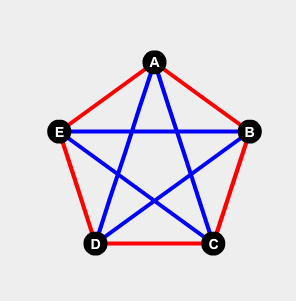
This is an example of a coloured K_5 that has no monochromatic 3-cliques.

Ok so five doesn’t work. Consider now K_6:

In essence we want to attempt to construct a graph without a monochromatic 3-clique. If we can’t then that must mean that all edge colourings of K_6 satisfy the conditions.

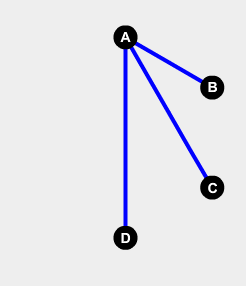
Choose an arbitrary vertex (for simplicity, choose A) and consider its edges to the five other vertices, then by the good old Pigeon Hole Principle, you are guaranteed that there are at least three edges of the same colour.

Without loss of generality, let us say that there are (at least) 3 blue edges.

Now we look at how the other 3 edges connecting B, C, D can be drawn and attempt to draw them such that there is no 3-clique.

Firstly, the edge between B and C cannot be blue or else the clique A, B, C will all be blue. Similarly for the edges between C, D and B, D.

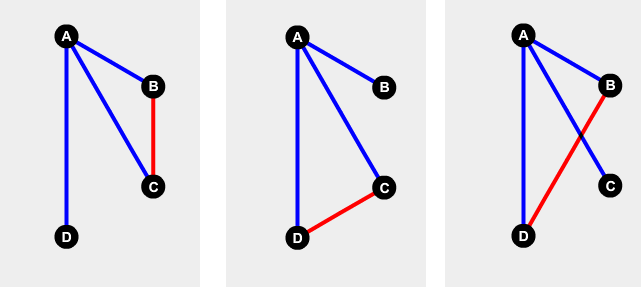
This forces us to colour all three of those edges red. But hang on! Three red edges sounds very much like a red 3-clique. Indeed we have been forced to construct a red 3-clique.

Therefore, any complete graph on six vertices must contain at least one monochromatic 3-clique.

Q.E.D

Notice that I have been very careful in saying 3-clique. This is because (as all of mathematics) it can be generalised:

We define the Ramsey number R(m,n) as being the minimum number of vertices (R) such that the complete graph on R vertices is guaranteed to have either a red m-clique or a blue n-clique.

It is trivial to see that R(m,n) = R(n,m) and slightly less trivial (but still quite easy) to see that R(m,2)=m.

Other than this, some values for low numbers are known (R(4,4) = 18, R(4,5) = 25) and a few interesting bounds can be made. And that is it.

Very little is known for higher numbers. We know R(5,5) is bounded between 43 and 49.

This may seem astounding — 49 after all is not that big a number, why can’t we just use computers to brute force it?

Numbers in this field grow quickly: suppose we just want to computationally verify a lower bound. So we are considering a complete graph on 43 vertices, this gives 903 edges (43 choose 2), each edge can be coloured in 2 different ways (red or blue) giving approximately 10²⁷² different graphs to verify…

To give you a perspective of how stupidly big this number is:

Suppose every atom in the universe is actually a super powerful computer that can check a googol graphs every second (that is 10¹⁰⁰ per second) and they started running at the big bang, then by now they won’t even have made a dent into computing all the possibilities. In fact the number of graphs they would have checked is approximately equivalent to removing one atom from the observable universe.

Granted you can reduce the computations by saying that the problem is invariant under permuting the vertices or by swapping red and blue but that doesn’t quite cut it — it only reduces the number of graphs by two orders of magnitutdes, i.e about 10²⁷⁰.

Graham’s Number

Many articles and posts are floating around that give you a sense of awe to how large Graham’s number is but very few actually explain what it means and why it exists. I will try to do both.

In essence, Graham’s Number (GN) is the upper bound to R(4,4) with some additional restrictions.

The first restriction is that the graphs we are considering are N dimensional complete hyper-cubes. A 2-dimensional complete cube is just K_4, a 3-dimensional complete cube is pictured below, and so on. In general, an N-d complete cube is a graph with vertices on each vertex point of the hypercube (equivalently, all points {±1}ᴺ) and every vertex is connected to every other vertex via an edge. Note that the structure is isomorphic to the complete graph on 2ᴺ vertices.

The next is that we don’t want any old clique, we require that the cliques are coplanar (in the geometric sense) in the hyper-cube. That is, all 4 vertices of our clique must lie in the same plane.

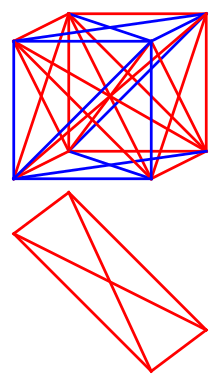
As of the writting of this article, it is known that the answer is greater or equal to 13 and less than GN (even though a much ‘smaller’ bound was given by Erik Lipka in his paper “Further improving of upper bound on a geometric Ramsey problem” arXiv:1905.05617).

Now how is GN defined? First we look at Knuth’s arrow notation, which is defined as such:

Firstly for positive integers a, b, a↑b = aᵇ. So for example, 3↑3 = 3³=27.

Next a↑↑b = a↑²b = a↑a↑a↑…↑a (where a is repeated b times). So 3↑²3 = 3↑3↑3 = 3²⁷ which is approximately 7.6 trillion.

We continue in this way: a↑³b = a↑↑a↑↑a↑↑….↑↑a (again, repeated b times).

So 3↑³3 = 3↑↑3↑↑3 = 3↑↑3²⁷ = (((3³)³)³…)³ where this ‘tower’ of threes is about 7 trillion threes tall. This is ‘scientifically’ known as off-the-charts big.

Okay, we are nearly there, I promise.

We start by defining g_1 = 3↑↑↑↑3 = 3↑⁴3 which is even more mindbogglingly bigger than the 3↑↑↑3.

Next we define g_2 via g_1 as being 3↑↑…↑↑3 where there are g_1 arrows. And more generally g_(n+1) = 3↑↑…↑↑3 with g_n arrows.

Recall that already with 2 arrows, we have a number slightly larger than the GDP of Japan (as of 2019 according to the IMF) or the number of miliseconds the average human lives for. With 3 arrows it already starts to fall out of comprehension, we have a stack of 3s that if we wrote out, would reach the sun. So imagine how big already g_1 is (spoiler: you can’t).

Graham’s Number is g_64.

Recall what the point of GN is: an upper bound the problem outlined above, a lower bound is 13.

To give you an idea of how stupidly, insanely, mind-bogglingly big Graham’s number is:

But don’t forget that even this number is huge, in reality, it is peanuts compared to infinity.

Note that the current upper bound given by Lipka mentioned above is merely 2↑↑↑5. To understand this, we start with a tower of twos: ((2)²)²…)² that is 65536 tall, call this number K, then construct a second tower of twos that is K twos tall. This is a much lower upper bound.

Now if like me, your brain is starting to hurt, I will leave you with a nice quote from a wonderful documentary about Paul Erdős (a major contributor to Ramsey theory)

Suppose aliens invade the earth and threaten to obliterate it in a year’s time unless human beings can find the Ramsey number for red five and blue five. We could marshal the world’s best minds and fastest computers, and within a year we could probably calculate the value. If the aliens demanded the Ramsey number for red six and blue six, however, we would have no choice but to launch a preemptive attack.