Previously, we were investigating circles centred at the origin. Our main goal was to understand how many rational points circles with different radiuses could contain. We call the point on the coordinate plane rational if both its coordinates are the rational numbers.

In the first article, we introduced the method for getting an infinite amount of rational points if the circle contains at least one rational point. We also proposed a statement that we can split all circles with centres in origin in two sets: circles that have zero number of rational points and an infinite amount of them. To prove this statement, we need to show that both sets are not empty, so it is necessary to find at least one circle without rational points.

We will use the method from the second article to show that there are no rational points on a circle with a radius square root of 3, and we will pose more questions to ourselves about the existence of rational points in other cases.

The Unusual Circle

The circle with radius equals to the square root of 3 is defined by the following equation:

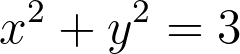
Let us look at the graph defined by this equation.

We know that the rational points are dense in the coordinate plane. It means we always can find another rational point that is lying between any two rational points on the plane. Size of them is less than the size of real points, but the plane still has numerous amount of rational points. Given this fact, it is hard to believe on a glance that this quadratic curve does not cross any of the rational points on a plane.

Let us pose a formal question that we are going to answer in this article. We want to show that there are no such whole numbers a, b, c, d that could satisfy the equality:

Also, pairs a, b and c, d should be co-prime, so it is impossible to reduce the fractions to lower terms.

We will try to transform this equation in the rational number to the equivalent equation, which we can solve in the whole numbers. It will allow us to use the power of modular arithmetic from the second article.

Tricks with divisibility

Let us multiply this equation on a common denominator of the terms in the left side of the equation:

After multiplication, we can move bc term from the left side to the right side and move b² out of the parentheses:

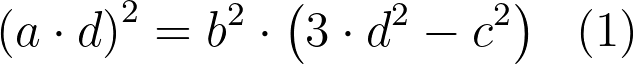
We see that b² divides the right side of the equation, so it also should divide the left side. If b² divides (ad)², so b should divide ad:

If b divides ad then we can rewrite ad as a product of b and some other whole number z:

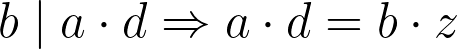
Let us substitute bz in the equation (1) as a replacement of ad and divide by b²:

Next, we move c² to the left side:

We have got an equation in the whole numbers, and from the definition we know that c and d are co-prime. Let us use this information to show that the whole number z should also be co-prime to c and d.

Suppose we know that some prime number p divides both z and c. It means that p² divides z² and с² at the same time. p² divides the left side of the equations, so that p² should also divide the right side:

However, this statement gives us a contradiction. The whole prime number p can not divide d because it would mean that c and d are not co-prime, and p² cannot divide the prime number 3, so it means there are no such prime p that divides z and c at the same time. We can follow the same steps for showing that there is no prime p such that p divides z and d.

Modular arithmetic comes into the field

We ended up with the following equation in the whole numbers:

We also know that z, c, and d are co-prime, so that at least two of them should be odd numbers. Now we are going to switch to the equation in terms of residue classes with modulo n equals to 4.

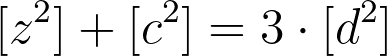
Let us assume that d is odd. It means that there is only one possible value of [d²]:

And if we multiply it by 3 we get:

But from the previous article, we know that it is impossible to find values for z and c such that:

So we get contradiction if we assume that d is odd.

Let us switch to the left side and assume that z is odd.

It also means that [z²] equals to 1 as with d, so we need to find c and d such that:

Let us show that this is also impossible. We can check every possible residue classes of d and c.

So z also can not be odd. We have got contradiction again.

Validation for c will be the same as for z.

So in the end, we showed that there are no whole solutions that satisfy the equation (2), and we know that it is equivalent to our initial statement, saying there are no rational solutions of the equation:

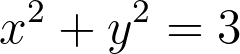
The further questions

In this article we proved the statement that there are only two types of circles centred at the origin, but what can we say about other circles?

Should we pose a theorem for every circle in the origin that has an irrational radius?

Or maybe we can use the generalised theory for showing it.

Will our statement about two types of circles hold for any circle on the coordinate plane?

Or we can find the circle with only one or two rational points.

Can we introduce a similar theory if we switch from circles to conics?

Or it becomes impossible to understand how many points the conic may have.

There are so many questions that we can pose, but it is impossible to include all answers in one article.

I am going to tackle most of these questions from above in the future articles, so I hope you enjoyed this story, and you are ready to see more articles in this series.