The Goldbach conjecture is one of the most captivating unsolved mysteries in mathematics. In this article, I will take you on a journey through time and mathematics.

I will present some other ways of looking at the conjecture than the original definition. Both visually and algebraically. We will prove an equivalence and investigate it a bit.

It’s All About the Primes

The Goldbach conjecture is about prime numbers so I believe that a word about them is in order.

Before jumping headfirst into one of the oldest and most “feared” questions in mathematics, let’s try to understand why we should care about questions involving prime numbers in the first place.

Recall that a prime number (or prime for short) is a whole number greater than 1 such that only 1 and the number itself divides it.

The first few primes are 2, 3, 5, 7, 11, …

In mathematics, and specifically in the field of number theory, we study the whole numbers and often we restrict our study to the positive whole numbers called natural numbers. That is, we are interested in the study of the numbers 1, 2, 3, 4, 5, … etc.

One approach in studying different objects in mathematics (and in nature as well) is to study the fundamental building blocks that all the objects comprise.

The fundamental theorem of arithmetic states that every natural number greater than 1 can be written uniquely as a product of primes. That is, every natural number has a unique set of primes that composes it. A unique prime factorization.

Of course, uniquely in this sense means “up to ordering of the factors".

For example, the number 6 can be written uniquely (as a product of primes) as 2⋅3, and 28 can be written uniquely as 2⋅2⋅7.

In that sense, one could argue that if we understood everything about the primes, then a lot of information about the natural numbers would follow.

In analogy, physicists study the fundamental building blocks of matter and forces like quarks, strings, quantum fields, the wave equation, etc. in order to understand nature and the laws that governs it, chemists study how the atoms like to combine into molecules to better understand the reactions between them, and biologists study the cell and its components to better understand life itself.

So we study primes because they are the building blocks of natural numbers.

An Innocent Looking Question

On 7 June 1742, the German mathematician Christian Goldbach wrote a letter to one of the greatest mathematicians of all time, Leonhard Euler — A letter that, even though it looked innocent at first glance, contained what was to become one of the greatest mysteries of mathematics.

In the letter he proposed the following conjecture:

Every integer that can be written as the sum of two primes can also be written as the sum of as many primes as one wishes until all terms are units.

We need to remember, of course, that back then, the number 1 was considered a prime, so when Golbach wrote “units”, he meant “ones”.

He then proposed a second conjecture in the margin of his letter.

Every integer greater than 2 can be written as the sum of three primes.

Euler replied in a letter dated 30 June 1742 and reminded Goldbach of an earlier conversation they had had, in which Goldbach had remarked that the first of those two conjectures would follow from the statement

Every positive even integer can be written as the sum of two primes

and in fact, this statement is equivalent to the one in the margin of Goldbach’s letter.

Somehow, in number theory, historically speaking, it is always in the margin the important stuff lies. Just ask Fermat!

Below is a picture of the original letter from Goldbach to Euler from 1742.

The conjecture in the margin of Goldbach’s letter is now called the Goldbach conjecture and in modern language, it states the following.

The Goldbach Conjecture:

Every even whole number greater than 2 can be written as the sum of two primes.

Let’s test this for the first few cases.

• 4 = 2 + 2
• 6 = 3 + 3
• 8 = 3 + 5
• 10 = 3 + 7 = 5 + 5

Note that in some cases, there is more than one way to write the number as a sum of two primes. The conjecture says nothing about that, so it’s allowed, of course.

This conjecture has been an inspirational source for many mathematicians along the way, and many tools have been created in order two study this problem. However, it has defeated the best mathematicians in the world for almost 300 years and it remains unsolved to this day.

Euler himself stated:

That every even integer is a sum of two primes, I regard as a completely certain theorem, although I cannot prove it.

~Leonhard Euler

What Does the Conjecture Really Say?

In mathematics, you can often view statements and theorems from different angles and sometimes some angle gives a clearer view than the others. This is called equivalences. Before giving you one, I better tell you what that is.

Say you have two statements (expressions that are either true or false) A and B. To say that A and B are equivalent is to say that A implies B and B implies A i.e. if A is true then so is B and if B is true then so is A.

For example:

Let S be a subset of the real numbers. Then the two statements

A: “You can divide the number 1 by any number in S”

B: “0 is not in S”

are equivalent. Because suppose A is true. Then 0 cannot be in S since we cannot divide 1 by 0. Therefore B is also true. Conversely, assume B is true. Then we can divide the number 1 by any number in S because the only real number that we can’t divide 1 by, is 0. Therefore A must be true.

Note that (at least for me) the statement B above is clearer and easier to understand than A is.

This is just a toy example of what it means for two statements to be equivalent. In real life, they tend to be much harder to prove though.

The Geometry of the Goldbach Conjecture

Let’s try to understand what the conjecture really looks like.

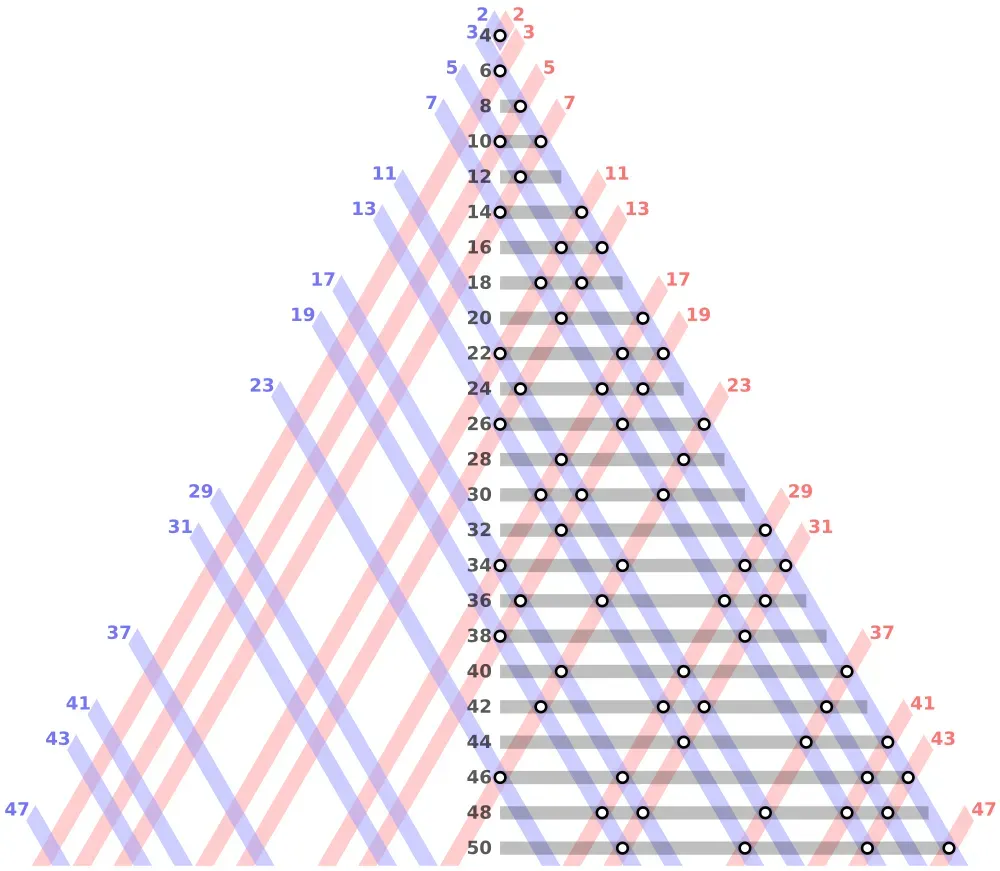
That a number is even of course means that it is divisible by 2. And what does it then mean that the sum of two numbers is even? Well, we can view it geometrically by first noting that the statement p + q = 2n is equivalent to (yes in the above sense) (p+q)/2 = n. That is, the average of p and q is equal to n.

What does this say geometrically? Imagine the real line (embedded in the real plane) with 0 in the middle, negatives on the left, and positives on the right containing all the numbers as you usually think of them.

Then the above statement says that there exists a circle with center n (on the real line) that intersects the real line in p and q. That is, p and q lie equidistant from n on the number line. We will use this fact a little later and remember that this is true for any numbers p and q, not just for primes.

To summarize: Let p, q, and n be any natural numbers satisfying p + q = 2n then p and q lie symmetrically (equidistant) around n.

In this language, the Goldbach conjecture says:

For every whole number n ≥ 2 there exists a circle in the plane with center n and radius r such that 0 ≤ r ≤ n-2 and either n is prime and r = 0 or the circle intersects the real line in two prime numbers.

This is in fact equivalent to the Goldbach conjecture.

Now, is that a better way of looking at it? Well, maybe not, but at least it gives a nice geometric intuition about the problem. It says that there is an underlying symmetry between the whole numbers and the prime numbers.

Note that we don’t really need the circles but only that the numbers lie symmetrically around n on the line. However, I think that the circles give a nice geometric intuition and picture of what’s going on.

In the next section, we let ourselves get inspired by this view and actually prove yet another equivalence.

The Semiprime Equivalence

In number theory, we tend to divide problems up into two groups. Problems of additive nature and problems of multiplicative nature. For example, that we can prime factorize a natural number greater than 1 is a multiplicative problem. The twin prime conjecture and the Goldbach conjecture are more additive in nature.

What if there was a more multiplicative way of looking at the Goldbach conjecture? An equivalence of some sort.

Before showing you one, recall that a semiprime is a natural number that is the product of exactly two prime numbers.

The first few semiprimes are 4, 6, 9, 10,…

Semiprimes are not talked about as much as primes but in a certain sense, they are “close” to being prime which in itself makes them worthy of study. I claim that the following statement is equivalent to the Goldbach conjecture.

Statement 1:

For all n ≥ 2, there exists a whole number m such that 0 ≤ m ≤ n-2 and n² - m² is a semiprime.

Let’s prove the following proposition:

Proposition

Statement 1 is equivalent to the Goldbach conjecture.

Proof:

Assume the Goldbach conjecture and suppose we are given a whole number n ≥ 2. We Then by assumption 2n = p + q for some prime numbers p and q.

Assume without loss of generality that p ≤ q, then by the above discussion, there exists a whole number m such that 0 ≤ m ≤ n-2 and

• p = n - m
• q = n + m

This implies that n² - m² = (n - m)(n + m) = p⋅ q.

So n² - m² is a semiprime.

Conversely, assume statement 1 and suppose we are given a number 2n with n ≥ 2. We need to show that 2n can be written as a sum of two primes.

By assumption, we can find a number m with 0 ≤ m ≤ n-2 and n² - m² a semiprime. And since n² - m² = (n - m)(n + m) then both n - m and n + m must be prime numbers but then we have

2n = (n - m) + (n + m), thus 2n is a sum of two primes.

Q.E.D.

This means of course that if you prove Statement 1, then by implication you have proved the Goldbach conjecture (and vice versa).

Visualizing the Conjecture

What does this mean visually?

It turns out that you can think of whole numbers as boxes in 1, 2, or 3 dimensions built from small cubes.

For example, the number 6 can be built with 1 × 6 cubes in 1 dimension (as a long stick) or 2 × 3 cubes in two dimensions,

27 (which of course is not a semiprime) can be built with e.g. 3 × 9 cubes in two dimensions or with 3 × 3 × 3 cubes in three dimensions (so literally a cube).

Imagine that you have a square of these small cubes in two dimensions.

Then the above way of looking at the Goldbach conjecture says that no matter how big your square is, you can remove some smaller square (or not) such that the resulting shape can only be rebuilt into a box in 1 or 2 dimensions but not 3.

If you look at it from above it would look like the following picture.

The Importance of Curiosity and Abstractions

The study of prime numbers is important because, as mentioned in the beginning, they build up all other numbers and this philosophy has carried on for more than 2000 years, but what the Greeks didn’t know back then, was that 2300 years later, information about the prime numbers would play a crucial role in cybersecurity and online transactions — Euclid was great, but he couldn’t have foreseen the invention of the internet!

This shows that even though the study of some pure mathematical subjects may have no direct applications to society or impacts on the way we live our daily lives, it may just be that we started an avalanche that will transform the way humans live 2000 years from now.

Curiosity is the most important gift in science.