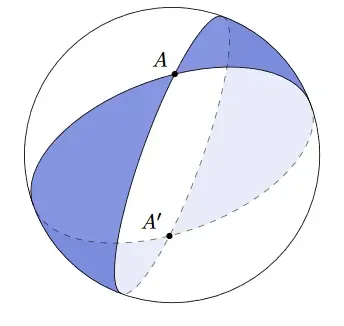
A visual proof of the Gauss Bonnet Theorem for triangles on spheres!

Spherical geometry is a beautiful, and very visual, area of mathematics, with weird properties (such as that the angles of triangles don’t sum to 180 !!!).

Understanding a little bit of Spherical Geometry

The Gauss-Bonnet Theorem for triangles on spheres is a special, but rather beautiful, case of the more general Gauss-Bonnet Theorem.

The theorem can be understood visually

First, let’s visualise what a triangle on a sphere is. Below are two visualisations of the same triangle.

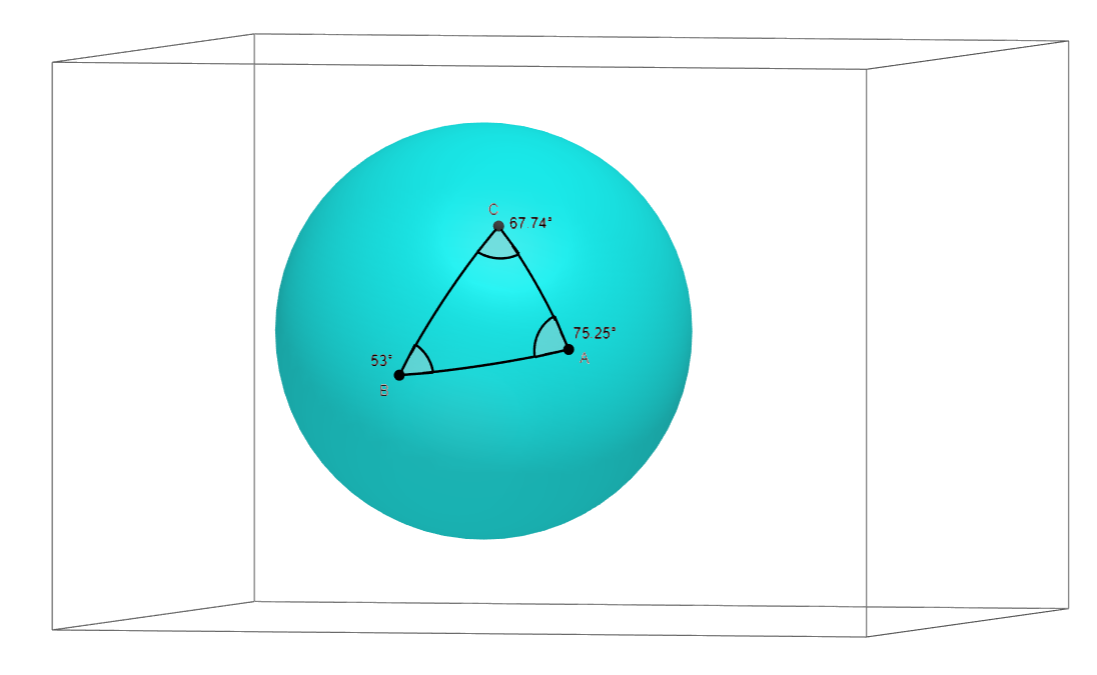
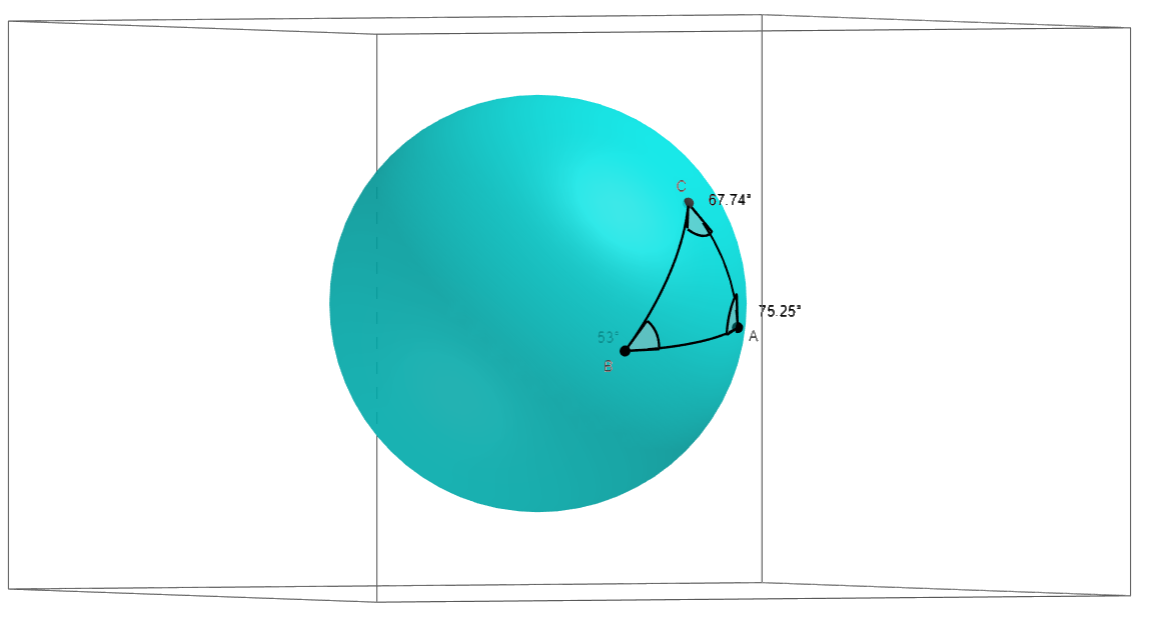
To draw a triangle on a sphere, we pick 3 points, and then we draw lines connecting them. But drawing a ‘line’ on a sphere isn’t an obvious concept. So instead we draw a curve between the two points. Visually, its the curve you’d expect to draw if you tried to make the curve as short, or as ‘direct’, as possible.

We then consider the angles on the triangle. But this triangle is on a sphere, not on a flat sheet of paper! How do we work out the angle?

There is an intuitive answer. As the curves connecting the endpoints of the triangle get closer together, they look more and more ‘straight’. In the picture below, we zoom in really close to illustrate this.

Visually, this should give you the sense that we can make sense of the idea of an angle for a triangle on a sphere.

Optional extra: defining angles for triangle

If you’re interested in how to define the angles on spheres then a slightly more detailed approach is below. But the intuitive understanding is enough for the rest of the proof, so its not essential to do this section to understand the rest.

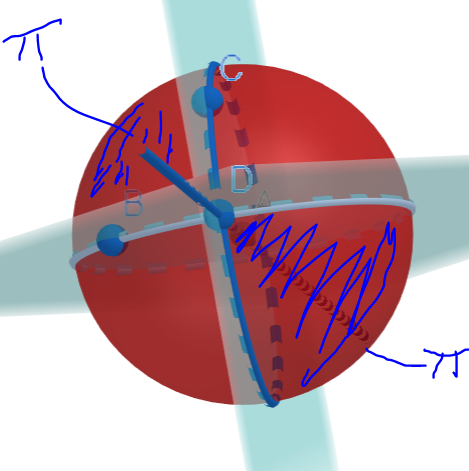
Below, we take 3 points on a sphere, B, C, D and create a triangle. We then create 3 planes, using the centre of sphere and (C,D), (D,B) or (C,B).

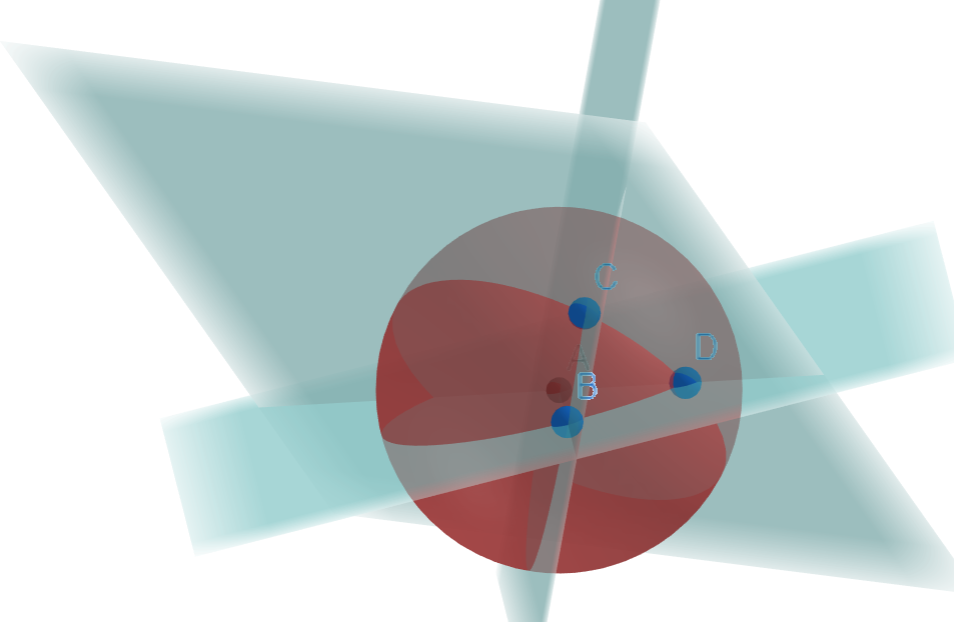
The above picture is a bit scary, so the picture below shows how we create a plane using two of the points and the centre.

Then we define the angle between two sides using the planes: as planes are ‘flat’ objects, like sheets of paper in 3D space, we can define the angle between two planes.

Stating the Theorem

Finally we state the Theorem! But, one last thing. We measure angles in radians. That just means that everything is measure compared to ‘2*pi’. We say 2pi radians is the same as 360 degrees. So pi radians is the same as 180 degrees. And pi/2 radians is the same in 90 degrees. This is similar to how you can measure distance in terms of kilometres, but you can also measure distance in terms of miles.

However, if you feel much more comfortable using degrees, I will also give the formula using degrees. (I prefer radians because all the results become so much prettier)

We label the three angles in the triangle a, b, c. Then we get the following formula for the area of the triangle:

Or, using degrees instead of radians

A surprising consequence

This formula for the area of the triangle already has some amazing consequences. Using the formula when the angles are measured in degrees, if the sum of the angles was equal to 180 degrees, then the area of the triangle would be 0. This is obviously nonsensical. As the area is greater than zero, we can conclude that the sum of the angles of spherical triangle must be greater than 180 degrees, or (measured in radians), greater than pi radians.

Proof

Finally, we prove the theorem!

First we find the area of a much simpler object. This object we call a ‘(spherical) lune’.

We take two planes, and look at the area of the sphere ‘captured’ between them. The area of an entire sphere is 4pi. So if the angle between them is, say, c radians, then the area captured between it is 4c. For instance, if the angle between our planes was a right angle, that is 90 degrees or pi/2 radians, then the area captured would be 2pi, or half the total area.

(However, note that if you use degrees the formula is a bit less elegant. We then have to normalise 90 degrees and adjust by a factor of pi, so the area, when using degrees is given by 4*pi*c/180, and when c=90 we get the area = 4*pi*90/180 = 2pi as before)

Ok, so we can find the surface area of a much simple shape. But what about our triangle?

Next we use a sneaky trick. We do the same as the above, but three times. When we shade this on the sphere below, we can see that a triangle is in the region which is shaded all three colours (which are merged to form a brownish colour)

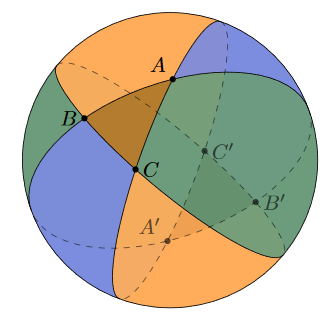
What happens when we sum the areas of each part? The triangle appears in all three of the spherical lunes, so its area is counted three times. So, if we sum the area of the lune, we get the total surface area of the sphere plus four times the area of our triangle. That’s because our triangle’s area is ‘double counted’ on each side, and there are two sides. Moreover, we know the area of each lune! That’s because the angle of the lune determines its area, and the angle of each lune in this case is simply the angle between two sides of the triangle.

Thus, we can conclude:

And we are done!

If you have any thoughts or improvements, please leave them in the comments below! I’m also newly on twitter, as ethan_the_mathmo.