Diving deep into the intricacies of mathematics is always an enjoyable thing. Most engineering undergraduates, like myself, are up for a good mind-bending problem any time of the day. Not only does it help sharpen the mind but also provides a gratifying experience that one can solve anything put on the table — what I can understand, I can solve.

But from the deep dark corners of mathematics, where even the theoreticians dare not enter, comes a devil dressed as a saint. It lures its prey with its simple looks and easy arguments. The petty prey starts with a blank paper and a pen. Nothing much happens on the first page, but it seems too simple to give up already. Eventually, the predator leads the gullible frosh to page two, followed by page three, four and five. The problem seems to clear bit-by-bit, but nothing concrete emerges out. He keeps working days, weeks, months. Eventually, it has been a year — and the progress is not any better than he had on page one.

Such is the devil named Collatz Conjecture.

Paul Erdős, possibly the most famous mathematician of all time, said that “Mathematics may not be ready for such problems”. Greatest mathematicians have given up their hands on this conjecture — rendering it the title of being infamous.

I have been a fan of this problem since I was 15, and I wasted a quarter of a year trying to crack a solution myself and failed miserably. But this week, I tried something different — instead of solving the problem, I analysed how the numbers ‘tumble down’, and the results were shocking.

The Problem

Before we analyse what I did, it is important to understand the problem itself.

The Collatz Conjecture, as stated by the brilliant mathematician Terence Tao is:

The Collatz map Col: N + 1 → N + 1 on the positive integers N + 1 = {1, 2, 3, . . . } by setting Col(N) equal to 3N + 1 when N is odd and N/2 when N is even, and let Col_min(N) := infn∈ N Coln (N) denote the minimal element of the Collatz orbit N, Col(N), Col2 (N), . . . . The infamous Collatz conjecture asserts that Col_min(N) = 1 for all N ∈ N + 1

If this seems like technical jargon, then here’s the layman version: Take anypositive integer. If it is even, divide it by 2. If it is odd, multiply the number with 3 and add 1. Whatever answer you get, do the same operations on the answer. Suppose, the number is 13. Then, the operations will be as follows:

13–40–20–10–5–16–8–4–2–1–4–2–1…

Eventually, for all numbers (in theory), the series ends at this loop of 4,2,1. Doesn’t matter if the starting number is 300, 3000 or 3 million — If you do the math correctly, you will reach 4,2,1. These result has been verified for numbers as big as 10¹⁸.

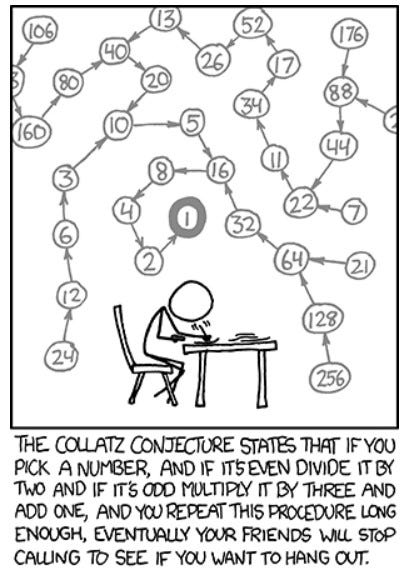
Looks simple, right? Well, no one on earth knows why this is happening. Why are these numbers converging to 1 and not flinging off to infinity? Why are there no such other loops where the values stop developing? Should governments stop math undergrads from consuming such problems? Well, these are some of the biggest questions, with answers unknown.

What is known, however, is that the point to solving this problem is knowing how these values reach some 2^n — That is the only way that any number may reach the loop of 4,2,1. Since we are always doing an ‘evening’ function on the odd numbers (any odd number multiplied by 3 is odd, adding 1 to it leads to an even number), I figured that we need to look at the odd numbers to reach even ones.

Hard Numbers

I coined the term hard numbers to define the last odd value any number reaches before it becomes 2^n. Hence, we refer to hard points as the points that have such a value that when the operation 3n+1 is performed, it renders a power of two.

The smallest hard number is 5. The second on this list is 21, followed 85, then 341 and so on. The general formula for finding a hard number is:

The primary aim of calculating these numbers is that any number except a power of two must reach a hard number before it converges to 1. This certainty of reaching a particular number exactly before becoming an exponent of two gives it a unique status towards understanding the problem.

I figured from these numbers that there has to be a frequency distribution that spans across these hard numbers. As the numbers increase, there must be a pattern that emerges for hard numbers, which might help us solve this problem. So I did a quick back-of-the-envelope calculation, wrote some iterative code and saw the results. I ran it for the first 1000 numbers and noted the distribution — I repeated this exercise till a max of first 50,000 numbers. I did a total of more than 180,000 iterations.

My prediction was that as the numbers grow, so must the frequency of larger hard numbers. After all, larger numbers must end at larger numbers and converge.

But boy, was I wrong.

The Results

The results were staggering. Of all the values till 50,000, around 47,000 numbers hit a rock bottom of 5, before becoming 16. What it means, is that over 94% of the numbers reached 5 before becoming a power of two!

Not only that, but for the first 10,000 numbers, the percentage of values reaching 5 increased, rather than decreasing! The weightage of 5 never went below 92%, and hence the most common hard number is 5.

The numbers 10,000 100,000 and 1,000,000 all reach 5 before becoming a power of two!

Moreover, the frequency distribution is very asymmetric. 5 is generated over 92% of the time. The numbers reaching the hard number 85 are 10 times more than numbers reaching 21, which occurs more often than 1365, but not as much as 341. Why is that the case, I’ve no idea!

Here is a pie chart of the frequency distribution:

As you can see — 5 is the most prominent value, followed by 341, which is a bigger slice than 85, which is still bigger than 21. The biggest hard number less than 10,000–5461 was reached only twice.

This wild behaviour of these seemingly un-related frequencies shows that the pattern of frequencies between hard numbers needs a lot more attention. Why this asymmetry? Why is 5 the most prominent case? Does 5 remain the most frequent hard number even beyond a million iterations? These questions are excellent food for thought.

Conclusion

All my observations have proved, is that Collatz is a very, very weird problem.

To sum up: We understood the problem, tried to pin-point values that matter, and saw some surprising results that had no relational attributes. The answer only raised more problems. The fact that numbers tumble down to such small values shows that it is not as much about reaching a proper power of two, as they are about reaching an odd value that is the brother of the power of two.

Innumerable questions might pop from these numbers, and I hope one day we know the answers to all these questions. Till then, one must have to fight with the dragon with his sword sharpened and back straight — it breathes the fire of alluring vacuum. All I can hope is that someday, some warrior might do the job. Till that day, all there is is a bunch of questions.

You can find the full data related to this experiment here. If you liked this article, consider following me on Medium, Twitter or LinkedIn.

You can check out my podcast here!