The Absent-Minded Father of Cybernetics, Norbert Wiener

“When we met, was I walking to the faculty club or away from it? I’m wondering, because in the latter case I’ve already had my lunch”

American mathematician Norbert Wiener (1894–1964) was by all accounts, a very peculiar man. After graduating from high school at 11 years old, he entered Tufts College and within three years was awarded an A.B. in mathematics. Before the age of 18, Harvard had awarded him a Ph.D. for his dissertation in mathematical logic. Described by author Sylvia Nasar as:

“An American John von Neumann, a polymath of great originality who made stunning contributions in pure mathematics and then embarked on a second and equally astounding career in applied mathematics”

Wiener would be the man to give modern meaning to the word ‘feedback’ through his invention of cybernetics (the study of regulatory systems) which has since birthed important subfields such as artificial intelligence, robotics, neuroscience, computer vision and others.

His career achievements notwithstanding, Wiener is perhaps even more so remembered for his extraordinary personality. According to one of his biographers, the great man spent 30 years “wandering the halls of MIT, like a duck”, one of its most well-regarded and renowned professors of mathematics, especially known for his absent-mindedness:

“His office was a few doors down the hall from mine. He often visited my office to talk to me. When my office was moved after a few years, he came in to introduce himself. He didn’t realize I was the same person he had frequently visited; I was in a new office so he thought I was someone else.”— Phyllis L. Block

“He went to a conference and parked his car in the big lot. When the conference was over, he went to the lot but forgot where he parked his car. He even forgot what his car looked like. So he waited until all the other cars were driven away, then took the car that was left.” — Howard Eves

This is the story of the “myopic parody of an absentminded professor”, Dr. Norbert Wiener.

Early Life (1894–1909)

Norbert Wiener was born in Missouri in 1894 to Leo Wiener and Bertha Kahn, both of Jewish origin. His father Leo was by the time Norbert was born already a renowned scholar of history and languages, having attended the University of Warsaw in 1880 and later the Friedrich-Wilhelm-Universtät in Berlin. A polyglot, his father knew languages well. As Norbert recalled in his autobiography Ex Prodigy (1953) multilinguism was the custom at the time when his father grew up:

“German was the language of the family, and Russian that of the State. [...] He learned French as the language of educated society; and in Eastern Europe, especially Poland, there were still those who adhered to the Renaissance tradition and used Italian as another language of polite conversation.”

His father however took the custom to an extreme. By the time he was ten years old, Leo reportedly spoke equally as many languages. Over the course of his life, he would reportedly master a total of 34, including Gaelic, multiple American Indian languages as well as the language spoken by the Bantu people of Sub-Saharan Africa.

Leo met Norbert’s mother Bertha while working as a teacher in Kansas City and married her in 1883. Bertha was “a small, pretty woman, […] remembered as a practical, sociable and “folksy” housewife” by the people in the small town where she and her husband later settled. The two married in 1893, a year before Norbert was born. Their son was named after the leading man in Robert Browning’s dramatic poem In a Balcony.

Child prodigy

Even from his earliest years, Norbert showed signs of remarkable mental agility. At eighteen months old, as his father Leo recounted, Norbert learned the alphabet by watching his caretaker draw letters in the sand at a beach:

When he was 18 months old, his nurse-girl one day amused herself by making letters in the sand of the seashore. She noticed that he was watching her attentively, and in fun she began to teach him the alphabet. Two days afterward she told me, in great surprise, that he knew it perfectly.

His mother Bertha would read to Norbert from a very young age. By age three however, Norbert was the one reading to her. His father Leo — by then professor at Harvard University — would also tutor him on the floor of his study. Young Norbert loved science books and on his third birthday was given a copy of Wood’s Natural History, which he devoured. He was still below school age when his father’s training began. According to Wiener himself, at that point his schooling consisted mainly of informal lectures in his father fields of expertise (languages and literature) including the Greek and Latin classics, followed by Leo’s favorite German poets and philosophers as well as Darwin and Huxley. Norbert was not yet six years old.

Although his son was clearly gifted, Leo was also a strict tutor who upheld very high standards. When Norbert made mistakes, his father reportedly turned “extremely critical and harsh” as Wiener in his autobiography Ex Prodigy (1953) later recalled:

Algebra was never hard for me, although my father's way of teaching it was scarcely conducive to peace of mind. Every mistake had to be corrected as it was made. He would begin the discussion in an easy, conversational tone. This lasted exactly until I made the first mathematical mistake. Then the gentle and loving father was replaced by the avenger of blood.

Despite still being physically immature, by the time Norbert was seven his father had placed him in the progressive Peabody School in Cambridge, Massachusetts. His young age notwithstanding, he was initially placed in the third grade before swiftly being advanced to the fourth, but still did not fit in. His reading skills were excellent, but, paradoxically, his aptitude for mathematics appeared lacking. Upon learning that this was the result of Norbert’s boredom from “routine drills of memorization”, Leo subsequently pulled his son back out of school and continued on for another three years with his “radical experiment in home schooling” (Conway and Siegelman, 2005).

The Most Remarkable Boy in the World (1906)

The world first came to know of Norbert Wiener on October 7th 1906, when a portrait of the boy genius adorned the front page of Joseph Publitzer’s New York Worldunder the inconspicuous headline “The Most Remarkable Boy in the World”. The featured article included interviews with both Norbert and his father, in a tone seemingly approving of his father’s unconventional approach to early child development:

The boy, Norbert, had learned his letters at eighteen months. Under his father's tutelage, he began reading at three, reciting in Greek and Latin at five, and in German soon after. At seven he took up chemistry, by nine algebra, geometry, trigonometry, physics, botany, and zoology, and that fall, at eleven, he had entered Tufts College in the neighboring town of Medford after only three and a half years of formal schooling.

- Excerpt, "The Most Remarkable Boy in the World" in New York World, October 7th (1906)

Norbert’s Relationship with Leo

“My closest mentor and dearest antagonist”

As described by physicist Freeman Dyson (1923–2020) in his essay “The Tragic Tale of a Genius” in The New York Review of Books (2005):

"While he was growing up and trying to escape from his notoriety as a prodigy at Tufts and Harvard, Leo was making matters worse by trumpeting Norbert's accomplishments in newspapers and popular magazines" — Freeman Dyson

Indeed, Norbert’s father trumped his educational ideas publicly, in addition to the New York World article, in issues of the Boston Evening Record, the American Journal of Pediatrics and American Magazine. Indeed, Leo Wiener “made no bones about his intentional molding of Norbert and his sisters to make them geniuses” (Heims, 1980):

Professor Leo Wiener, of Harvard University [...] believes that the secret of precocious mental development lies in early training. [...] He is the father of four children, ranging in age from four to sixteen; and he has had the courage of his convictions in making them the subjects of an educational experiment. The results have [...] been astounding, more especially in the case of his oldest son, Norbert.

- Excerpt, American Magazine, July (1911)

Regarding his methods, Leo’s public accounts differ significantly from those which he gave his son. For instance, in reading Norbert’s fathers’ own account of how his children came to be so talented, one gets the sense that praise and acknowledgement of his children’s abilities were not a large part of his philosophy (Heims, 1980):

“It is nonsense to say, as some people do, that Norbert and Constance and Bertha are unusually gifted children. They are nothing of the sort. If they know more than other children of their age, it is because they have been trained differently.”

“Norbert is lazy and doesn’t study as much as the average boy his age” — Leo Wiener, 1906

More than anything, from Norbert’s own writing one gets the sense that he was indeed rather negatively affected by his fathers’ claims: (Wiener, 1953):

I felt that Father himself was not immune to the temptation to grant interviews to the slicks about me and my training [...]. In these interviews, he emphasized that I was essentially an average boy who had the advantage of superlative training.

This image of having been “created” by one’s father, combined with a lack of acknowledgement both of his talents, efforts and sacrifices, left a lasting impression on Wiener. “It rendered me more diffident as to my own ability that I would have otherwise been even under my father’s scolding.”

“In short, I had the worst of both worlds”

However, as clear from the interview with Leo in the New York World article, his father indeed did in fact know how gifted his son was, even though he was loathed to admit it to Norbert:

“I hate to talk about the boy, not because I am not proud of him but because it might get to his ears and spoil him. He has a keen analytical mind and a tremendous memory. He doesn't learn by rote, as a parrot might, but by reasoning.”

Education (1903–1913)

Following his father’s homeschooling, Norbert entered Ayer High School in 1903 at the age of nine, and was soon advanced even further:

It soon became clear that the greater part of my work belonged to the third year of high school, so when the year was over I was transferred to the senior class.

Following his graduation in 1906, his father “decided to send […] him to Tufts College rather than risk the strain of the Harvard entrance examinations”. Norbert, by then twelve years old, as always abided diligently.

Tufts University (1906–1909)

The young Wiener entered Tufts College in Massachusetts in the fall of 1906. There, he studied Greek and German, physics and mathematics, in addition to biology:

In spite of this interest in biology, it was in mathematics that I was graduated. I had studied mathematics every year in college […] found calculus and differential equations quite easy, and I used to discuss them with my father who was thoroughly oriented in the ordinary college mathematics.

He graduated cum laude with an A.B. degree in 1909, at 14 years of age.

Harvard University (1909–1913)

“I was nearly fifteen years old, and I had decided to make my try for the doctor’s degree in biology”

After graduating from college, Wiener went on to enter graduate school at Harvard University (where his father worked ) to study zoology. This despite the objections of Leo, who “was rather unwilling to concur in it. He had thought it might be possible for me to go to medical school” (Wiener, 1953). However, the emphasis on laboratory work combined with Wiener’s poor eyesight made zoology a particularly difficult specialization for him. His rebellion was not long lasting, and after a time, Wiener decided to follow his father’s advice and instead take up philosophy.

As usual the decision was made by my father. He decided that such success as I had made as an undergraduate at Tufts in philosophy indicated the true bent of my career. I was to become a philosopher.

Wiener was offered a scholarship to the Sage School of Philosophy at Cornell University, and transferred there in 1910. However, after a “black year” (Wiener, 1953) of feeling insecure and out-of-place, he transferred back to Harvard Graduate School in 1911. Originally intending to work with philosopher Josiah Royce (1855–1916) for his Ph.D. in mathematical logic, due to the latter’s onset illness, Wiener had to recruit his former professor at Tufts College — Karl Schmidt — to take his place. Schmidt, who Wiener himself later stated was “then a young man, vigorously interested in mathematical logic” was the person who inspired him to investigate a comparison between the algebra of relatives of Ernst Schroeder (1841–1902) and that of Whitehead and Russell’s Principia Mathematica (Wiener, 1953):

There was a lot of formal work to be done on this topic which I found easy; though later, when I came to study under Bertrand Russell in England, I learned that I had missed almost every issue of true philosophical significance. However, my material made an acceptable thesis, and it ultimately led me to the doctor's degree.

His dissertation in philosophy, highly mathematical, was in formal logic. The essential results of his dissertation were published the following year in the 1914 paper “A simplification in the logic of relations” in the Proceedings of the Cambridge Philosophical Society. The coming fall, Wiener traveled to Europe to do postdoctoral work in the hopes that he might eventually land a permanent position on the faculty of one America’s most prominent universities.

Postdoctoral Work (1913–1915)

Following his doctoral dissertation, defense and graduation from Harvard, Wiener — then 18 years old — was awarded one of the school’s prestigious one-year graduate fellowships to study abroad. His chosen destination was Cambridge, England.

Cambridge University (1913–1914)

“Leo Wiener hand-delivered his son to Bertrand Russell”

Norbert Wiener first arrived at Trinity College, Cambridge in September of 1913. Traveling with him was his entire family, spearheaded by his father Leo who had seized on the opportunity to take a year of sabbatical from Harvard and join his son in Europe. As Conway & Siegelman (2005) describe, “Young Wiener strode through the great gate of Trinity College, Cambridge, the Mecca of modern philosophy and the new mathematical logic, with his father in lock-step behind him”.

Wiener went to Cambridge to continue his study of philosophy with one of the authors of the Principia Mathematica which had been the focus of his dissertation at Harvard. Lord Bertrand Russell (1872–1970) — at that point in his early forties — was by 1913 considered the foremost philosopher of the Anglo-American world following the praise of his’ and Alfred North Whitehead’s monumental three-volume work, published in 1910, 1912 and 1913. The Principia or “PM” as it is often known, was at that point the most complete and coherent piece of mathematical philosophy to date. Renowned still for its rigor, the work among other efforts, infamously grounded the theory of addition to logic by proving, in no less than thirty pages, the validity of the proposition that 1+1 = 2.

Despite having been brought up at the heft of a polyglot “Harvard Don”, Wiener’s first impression of Russell’s fierce personality left something to be desired, as he would soon communicate to his father in letter-form:

Russell’s attitude seems to be one of utter indifference mingled with contempt. I think I shall be quite content with what I shall see of him at lectures

Russell’s impression of Wiener, or at least what he let him on to believe, appeared mutual. “Apparently, young Wiener did not “sense data” or do philosophy the way the titan of trinity prescribed it” (Conway & Siegelman, 2005):

Excerpt, letter from Norbert to Leo Wiener (1913)
”My course-work under Mr. Russell is all right, but I am completely discouraged about the work I am doing under him privately. I guess I am a failure as a philosopher [...] I made a botch of my argument. Russell seems very dissatisfied [...] with my philosophical ability, and with me personally. He spoke of my views as "horrible fog", said that my exposition of them was even worse than the views themselves, and [...] accused me of too much self-confidence and cock-sureness [...] His language, though he excused himself, it is true, was most violent.”

As with his father Leo, sadly, Russell’s opinion of Norbert, then 18 years old, was not as harsh as he himself had believed. In his private papers, Russell indeed noted approvingly of the boy and after reading Norbert’s dissertation commented that it was “a very good technical piece of work”, giving the young student a copy of the third volume of the Principia as a gift (Conway & Siegelman, 2005). 

Read more about Wiener and Russell’s relationship in a previous newsletter:

PrivatdozentOn Norbert Wiener's Relationship with Bertrand RussellNorbert Wiener (1894–1964) and Bertrand Russell (1872-1970) The later “Father of Cybernetics” Norbert Wiener (1894–1964) first arrived at Trinity College, Cambridge in September of 1913. Traveling with him was his entire family, spearheaded by his father Leo who had seized on the opportunity to take a year of sabbatical from his professorship at Harvard …Read more3 years ago · 6 likes · Jørgen Veisdal

The single most important take-away of Wiener from his work with Russell, however, was neither physical nor related to philosophy. Rather, it was the Lord’s suggestion that the young Wiener look up four papers from 1905 by physicist Albert Einstein, which he would later make use of. Wiener himself at time time singled out G.H. Hardy (1877–1947) as having the most profound influence on him (Wiener, 1953):

Hardy’s course […] was a revelation to me […] [in his] attention to rigor […] In all my years of listening to lectures in mathematics, I have never heard the equal of Hardy for clarity, for interest, or for intellectual power. If I am to claim any man as my master in my mathematical thinking, it must be G.H. Hardy.

In particular, Wiener credited Hardy for introducing him to the Lebesgue integral which “lead directly to the main achievement of my early career”.

Göttingen University (1914)

One experience richer, Wiener in 1914 continued to Göttingen University. He arrived in the spring after briefly stopping by to visit his family in Munich. Although only staying for a single term, his time there would be crucial to his further development as a mathematician. He assumed the study of differential equations under David Hilbert (1862–1943), perhaps the foremost mathematician of his era whom Wiener would later laud as “the one really universal genius of mathematics”.

Wiener remained in Göttingen until the outbreak of World War I in June of 1914, when he decided to return to Cambridge and continue his studies of philosophy with Russell.

Career (1915-)

Prior to being hired at MIT — an institution he would remain with for the rest of his life — Wiener worked a number of somewhat odd jobs, in various industries and cities in America. He officially returned to the United States in 1915, briefly living in New York City while continuing studies in philosophy at Columbia University with philosopher John Dewey (1859–1952). After that, he went on to teach philosophy courses at Harvard and next accepted a job as an engineer apprentice at General Electric. After that, he joined Encyclopedia Americana in Albany, New York after his father had secured him a job as a staff writer there, “convinced that with my clumsiness I could never really make good at engineering“ (Wiener, 1953). He also worked briefly for the Boston Herald.

With America’s entry into World War I, Wiener was eager to contribute to the war effort, and attended a training camp for officers in 1916, but ultimately failed to earn a commission. In 1917 he tried again to join the military, but was rejected due to his poor eyesight. The next year, Wiener was invited by mathematician Oswald Veblen (1880–1960) to contribute to the war effort by working on ballistics in Maryland:

I received an urgent telegram from Professor Oswald Veblen at the new Proving Ground in Aberdeen, Maryland. This was my chance to do real war work. I took the next train to New York, where I changed for Aberdeen

His experiences at the Proving Ground transformed Wiener, according to Dyson (2005). Before arriving there, he was a 24-year-old mathematical prodigy who had been discouraged away from mathematics due to the failings of his first teaching job at Harvard. Afterwards, he was re-invigorated by the applications of his teachings on real world problems:

We lived in a queer sort of environment, where office rank, army rank, and academic rank all played a role, and a lieutenant might address a private under him as ‘Doctor’, or take orders from a sergeant. When we were not working on the noisy hand-computing machines which we knew as ‘crashers’, we were playing bridge together after hours using the same computing machines to record our scores. Whatever we did, we always talked mathematics.

Mathematics

In his extensive bibliography of published writings, Wiener’s first two publications in mathematics appeared in the 17th issue of the Proceedings of the Cambridge Philosophical Society in 1914, the latter of which is now lost:

• Wiener, N. (1914). “A Simplification of the Logic of Relations”. Proceedings of the Cambridge Philosophical Society 17, pp. 387–390.
• Wiener, N. (1914). “A Contribution to the Theory of Relative Position”. Proceedings of the Cambridge Philosophical Society 17, pp. 441–449.

The first work, which regarded mathematical logic, was according to Wiener “presented on 23 February 1914 by G. H. Hardy” despite “exciting no particular approval on the part of Russell”. In the note, Wiener introduces the “dissymmetry between the two elements of an ordered pair by using the null set”. The work, which was the main result of his Ph.D. thesis at Harvard, proved how the mathematical notion of relations can be defined by set theory, thereby showing that the theory of relations does not require any distinct axioms or primitive notions.

Wiener’s most well known mathematical contributions were however mostly made between the ages of 25 and 50, in the years 1921–1946. As a mathematician, Chatterji (1994) singles out Wiener’s skillful utilization of the Lebesgue type integration theory (which Hardy had introduced him to in Cambridge) as a unique hallmark of his art. The Lebesgue integral extends the traditional integral to a larger class of functions and domains.

Following the end of World War I, Wiener tried to secure a position at Harvard, but was rejected, likely to the university’s anti-semitism at the time, often attributed to the influence of Department Head G. D. Birkhoff (1884–1944). Instead, Wiener assumed the position of lecturer at MIT in 1919. From that point on, his research output increased significantly.

In the first five years of his career at MIT, he published 29 (!!) single-authored journal papers, notes and communications in various subfields of mathematics, including:

• Wiener, N. (1920). “A Set of Postulates for Fields”. Transactions of the American Mathematical Society 21, pp. 237–246.
• Wiener, N. (1921). “A New Theory of Measurement: A Study in the Logic of Mathematics”. Proceedings of the London Mathematical Society, pp. 181–205.
• Wiener, N. (1922). “The Group of the Linear Continuum”. Proceedings of the London Mathematical Society, pp. 181–205.
• Wiener, N. (1921). “The Isomorphisms of Complex Algebra”. Bulletin of the American Mathematical Society 27, pp. 443–445.
• Wiener, N. (1923). “Discontinuous Boundary Conditions and the Dirichlet Problem”. Transactions of the American Mathematical Society, pp. 307–314.

The Wiener Process (1920-23)

Wiener first became interested in Brownian motion when was in Cambridge studying under Russell, who directed him to the “miracle year” work of Albert Einstein. In his 1905 paper Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhended Flüssigkeiten suspendierten Teilchen (“On the Motion of Small Particles Suspended in a Stationary Liquid, as Required by the Molecular Kinetic Theory of Heat”), Einstein modeled the irregular motion of a pollen particle as being moved by particular individual water molecules. This “irregular motion” had first been observed by botanist Robert Brown in 1827, but had not yet been investigated formally in mathematics.

Wiener approached the phenomenon from the perspective that “it would be mathematically interesting to develop a probability measure for sets of trajectories” (Heims, 1980):

A prototype kind of problem Wiener considered is that of the drunkard's walk: a drunk man is at first leaning against a lamp post; he then takes a step in some direction-it may be a short step or a long step; then he either stands still maintaining his balance or takes another step in some direction; and so on. The path he takes will in general be a complicated path with many changes in direction. 

[...]

Assuming the man has no a priori preference for any particular direction or particular step size and may move fast or slowly according to his whim, is there some way to assign a probability measure to any particular set of trajectories?

- Excerpt, John von Neumann and Norbert Wiener by Steve Heims (1980)

Wiener extended Einstein’s formulation of Brownian motion to describe such trajectories, and so established a link between the Lebesgue measure (a systematic way of assigning numbers to subsets) and statistical mechanics. That is, Wiener provided the mathematical formulation for describing the one-dimensional curves left behind by Brownian processes. His work, now often referred to as the Wiener process in his honor, was published in a series of papers developed in the period 1920–23:

• Wiener, N. (1920). “The Mean of a Functional of Arbitrary Elements”. Annals of Mathematics 22 (2), pp. 66–72.
• Wiener, N. (1921). “The Average of an Analytic Functional”. Proceedings of the National Academy of Sciences 7 (9), pp. 253–260.
• Wiener, N. (1921). “The Average of an Analytic Functional and the Brownian Movement”. Proceedings of the National Academy of Sciences 7 (10), pp. 294–298.
• Wiener, N. (1923). “Differential Space”. Journal of Mathematics and Physics 2, pp. 131–174.
• Wiener, N. (1924). “The Average Value of a Functional”. Proceedings of the London Mathematical Society 22, pp. 454–467.

As Wiener himself testified, although neither of these papers solved physical problems, they did however provide a robust mathematical framework which was later used by von Neumann, Bernhard Koopman (1900–1981) and Birkhoff to address problems in statistical mechanics originally posed by Willard Gibbs (1839–1903).

Return to Göttingen (1924–1926)

On the strength of his work in the early 1920s, Wiener returned to Göttingen during the summers of 1924–26, the latter year as a Guggenheim scholar. The height of the so-called golden age of quantum physics, his stays overlapped the visiting stays of both von Neumann and Oppenheimer, the former of which he came to know personally and correspond with.

In the summer of 1925, Wiener lectured on his work to the assembled group of mathematicians at Göttingen, both on faculty and visiting, later writing home that Hilbert had described his work as sehr schön (“very beautiful”). Towards the end of the stay, the head of the mathematics department, Richard Courant (1888–1972), reportedly told him that if he came back the following year he would be given the position of visiting professor.

Wiener–Khinchin Theorem (1930)

Starting after his stay in Göttingen, Wiener also began working in applied mathematics, and in 1930 on so-called autocorrelation functions which provide the correlation between a signal and a delayed copy of that signal, as a function of its delay. The so-called Wiener-Khinchin theorem shows how the autocorrelation function Rₓₓ(τ) is related to the power spectral density Sₓₓ(f) via the Fourier transform:

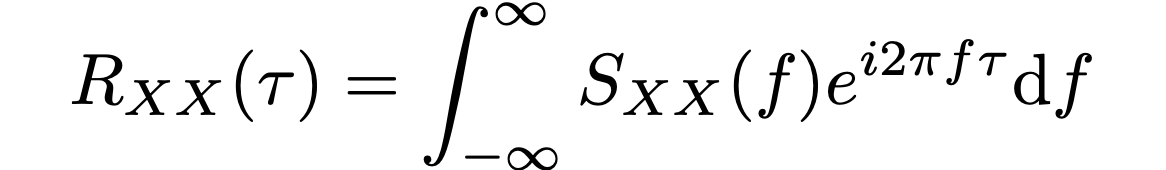
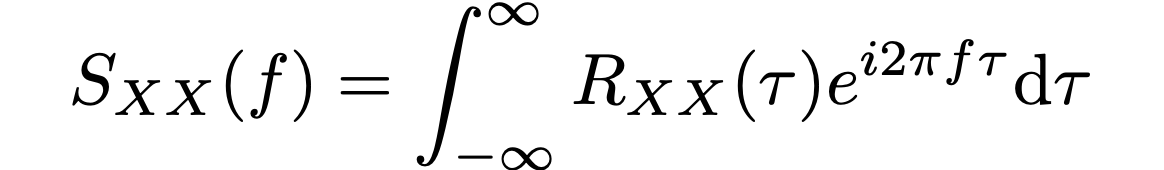
The result was published the same year Wiener was promoted to associate professor at MIT.

• Wiener, N. (1930). “Generalized Harmonic Analysis”. Acta Mathematica. 55, pp. 117–258.

Wiener’s Tauberian Theorem (1932)

Although by the early 1930s firmly engaged with signal processing and the early developments in electrical engineering, Wiener continued publishing papers in pure mathematics, including works in the analysis on Lebesgue spaces. Wiener’s tauberian theorem, published in 1932, provides the necessary and sufficient condition under which any function in L₁ or L₂ can be approximated by linear combinations of translations of a given function. His results appeared in the chapter

• Wiener, N. (1932). “Tabuerian Theorems”. Annals of Mathematics 33(1), pp. 1–100.

which Wiener begins by describing how:

“Numerous important branches of mathematics and physics concern themselves with the asymptotic behavior of functions for very large of very small values of their arguments”

His tauberian theorem regarded how to approximate such functions at very large values. The same year that the result was published, Wiener was promoted to full professor of mathematics at MIT.

Paley-Wiener theorems (1934)

Wiener supervised relatively few Ph.D. students. In Heims (1980) one of them, Norman Levinson (1912–1975), recounts his experience of collaborating with the great man:

He was a most stimulating teacher. He would actually carry on his research at the blackboard. As soon as I displayed a slight comprehension of what he was doing, he handed me the manuscript of Paley-Wiener for revision. I found a gap in a proof and proved a lemma to set it right. Wiener thereupon sat down at his typewriter, typed my lemma, affixed my name and sent it off to a journal.

- Excerpt, John von Neumann and Norbert Wiener by Heims (1980)

The Paley-Wiener theorems Levinson helped work on are a class of theorems which relate the decay properties of a function or distribution at infinity with analyticity of its Fourier transform. The work appeared in the book

• Wiener, N. & Paley, R. (1934). “Fourier Transforms in the Complex Domain”. American Mathematical Society Colloquium Publications 19.

Cybernetics

“Information is information, not matter or energy.”

The field that is now synonymous with Wiener’s name, came to be largely as a function of the Norbert’s interest in stochastic and mathematical noise processes, which are prevalent in both electrical engineering and communication theory. In a lecture entitled “Men, Machines, and the World About Them” Wiener describes how his pioneering work first came to be as the result of him trying to contribute to the war effort in the 1940s:

There were two converging streams of ideas that brought me into cybernetics. One of them was the fact that in the last war, when it was manifestly coming, but before Pearl Harbor at any rate, when we were not yet in the conflict, I tried to see if I could find some niche in the war effort at that time.

As Wiener himself states in the lecture, his first effort in the nascent theory of digital computing was not considered sufficiently immediate to be effective in that war, and so Wiener went looking for something else. His second initiative related to weaponry, specifically anti-aircraft defense:

I looked around for another thing and the great question that was being discussed at that time was anti-aircraft defense. It was the time of the Battle of England and the existence of the United States as a competent country, the survival of anybody to combat with Germany seemed to depend on anti-aircraft defense.

Now, the anti-aircraft gun is a very interesting type of instrument. In the First World War, the anti-aircraft gun had been developed as a firing instrument, but one still used range tables directly by hand for firing the gun. That meant essentially that one had to do all the computation while the plane was flying overhead. And actually by the time you got in position to do something about it, the plane had already dome something about it and wasn't there.

And so, Wiener goes on, “this lead to some very interesting mathematical theories. I had some ideas that turned out to be useful there”. He worked on the problem with Julian Bigelow (1913–2003). “Early in 1941, the two men took over an empty classroom on the second floor of the mathematics department, Building 2, Room 244, and set to work on the blackboard. Wiener outlined the fire control problem for his new collaborator” (Conway & Siegelman, 2005):

“Wiener and Bigelow considered the observer, gun, airplane, and pilot as an integrated, probabilistic system. The odds favored the pilot: in 1940 only one out of about 2,500 antiaircraft shells scored a hit. In a preliminary report, they explained how they intended "to place the analysis of the problem of prediction upon a purely statistical basis, by determining to what extent the motion of target is predictable on the basis of known facts and history, and to what extent the motion of the target is not predictable".

- Excerpt, Turing's Cathedral by George Dyson (2012)

An audio recording of Wiener’s lecture “Men, Machines, and the World About Them” from 1950 is available below. He begins speaking at 13:30:

Wiener Filter (1942)

Wiener’s work on the anti-aircraft fire-control problem resulted in his invention of a filter used to compute a statistical estimate of an unknown signal by using an input and filtering it to produce the estimate of an output. The filter built on several of Wiener’s previous results on integrals and Fourier transforms. Although developed at Radiation Laboratory at MIT, the result was published in a classified document. The first unclassified document describing the filter appeared in Wiener’s 1949 book “Extrapolation, Interpolation, and Smoothing of Stationary Time Series”.

As the war had ended in 1947 he was invited to a congress on harmonic analysis held in Nancy, France. The congress was organized by the secretive French mathematical society ‘Bourbaki’ in collaboration with mathematician Szolem Mandelbrojt (1899–1983), uncle of Benoit Mandelbrot (1925–2010), later discoverer of the Mandelbrot-set. While there, Wiener was offered to write a manuscript on the ‘unifying character of the part of mathematics which is found in the study of Brownian motion and telecommunication engineering’. The following year, he coined the neologism ‘cybernetics’ to denote the study of such ‘teleological mechanisms’. His manuscript would form the basis of the popular science work “Cybernetics: Or Control and Communication in the Animal and the Machine”, published by MIT Press/Wiley and Sons in 1948. The book was heralded (Wikipedia, 2020):

“A beautifully written book, lucid, direct, and, despite its complexity, as readable by the layman as the trained scientist, if the former is willing to forego attempts to understand mathematical formulas” — The Saturday Review (1949)

“Its scope and implications are breathtaking, and leaves the reviewer with the conviction that it is a major contribution to contemporary thought” — Philosophy of Science 22 (1955)

“One of the most influential books of the twentieth century, Cybernetics has been acclaimed as one of the ‘seminal works’ comparable in ultimate importance to Galileo or Malthus or Rousseau or Mill” — The New York Times (1964)

Personality

“He hardly seemed to know where he was”

His genius and extraordinary scientific contributions notwithstanding, Wiener is perhaps even better known for being famously eccentric. ”His appearance alone was remarkable […] He puffed on fat cigars. He waddled like a duck, a myopic parody of an absentminded professor.” Extremely near-sighted, the daughter of a colleague recalls Wiener being “A fascinating man, but such a child. Everybody took care of him. He used to sleep upstairs and nobody could go to sleep because of his snoring. It was horrible. Then, in the morning, he’d come padding into the wrong room, wandering around, because he couldn’t see” (Conway & Siegelman, 2005).

“While lecturing, he might be seen picking his nose “energetically,” with no apparent concern for his lack of social grace.”

Indeed, numerous accounts exist of various people interacting with and/or observing the great man, deep in thought, oblivious of his surroundings:

“It is vivid in my memory that Professor Wiener would always come to class without any lecture notes. He would first take out his big handkerchief and blow his nose very vigorously and noisily. He would pay very little attention to his class and would seldom announce the subject of his lecture. He would face the blackboard, standing very close to it because he was extremely near-sighted. Although I usually sat in the front row, I had difficulty seeing what he wrote. Most of the other students could not see anything at all.”

- Excerpt, Recollections of a Chinese Physicist by C.K. Jen (1990)

“On at least one occasion, he strode into the wrong classroom and delivered a rousing lecture to an audience of baffled students.”

In the essay collection “Mathematical Conversations - Selections from the Mathematical Intelligencer”, writer and mathematician Steven G. Krantz (1951-) recounts the following similar anecdote as additional evidence of Wiener’s modus operandi:

“When he walked the halls of MIT he invariably read a book, running his finger along the wall to keep track of where he was going. One day, engaged in this activity, Wiener passed a classroom where a class was in session. It was a hot day and the door had been left open. But of course Wiener was unaware of these details - he followed his finger through the door, into the classroom, around the walls (right past the lecturer) and out the door again.”

- Excerpt, Mathematical Conversations by Krantz (2001)

Biographers Conway & Siegelman (2005 p. 31) trace the permission for Wiener to indulge in his eccentricities back to his time as a postdoctoral fellow at Trinity College, Cambridge, where he first “saw all around him that stately bastion of high intellect and fading aristocracy a range of eccentricity that raised peculiarity to an art form”. Unlike Harvard, which Wiener later said “has always hated the eccentric and the individual”, in Cambridge “eccentricity is so highly valued that those who do not really possess it are forced to assume it for the sake of appearances”. The same sentiment was echoed by biographer Sylvia Nasar when describing the hot-house atmosphere of MIT’s math department in the 1950s:

“Showing off wasn't regarded as a crime if you knew your stuff. Lack of social graces was considered part and parcel of being real mathematicians. "Their attitudes were famously nonbourgeois, exhibitionistic, dissolute," Felix Browder recalled. If anything, all of them placed a certain premium on eccentricity and outrageousness.”

- Excerpt, A Beautiful Mind by Sylvia Nasar (1998)

“An MIT alumnus was driving in New Hampshire and stopped to help a tubby-looking man with a flat tire. He recognized Norbert Wiener and asked if he could help. Wiener asked if [the alumnus] knew him. Yes, he said, he had taken calculus with him. `Did you pass?' asked Wiener. `Yes.' `Then you can help me,' said Wiener. — Robert K. Weatherall, Vice President for Alumni at MIT”

Of course, his eccentricity served only to fuel the legend of Professor Norbert Wiener at MIT:

“MIT legends depicted him scribbling away furiously and ambidextrously on math department blackboards, solving simultaneous sets of complex equations, one with each hand” (Conway & Siegelman, 2005)

Depression

“Norbert Wiener was a great thinker and a tortured person.” — Benoit Mandelbrot

Gregarious as he was, Wiener’s mental life cannot have been a simple one. Starting when he was a child (in addition to being extraordinarily gifted) Norbert was often described as both careful and sensitive. He once described being “filled with gloom” from walking passed a hospital for “incurables” and even at an advanced age recalled how he was “instilled an abhorrence of suffering” from visiting a blacksmith whose toe had been crushed by a horse (Conway and Siegelman, 2005).

If a child or a grandchild of mine should be as disturbed as I was, I should take him to a psychoanalyst, not with confidence that the treatment would be successful in some definitive way, but at least with the hope that there might be a certain understanding and a certain measure of relief — Norbert Wiener

From reading the descriptions by people who knew Wiener and from his own autobiographies, it is clear that he struggled with feelings of inferiority. Likely not unrelated to his upbringing at the hands of his father Leo, these feelings extended beyond purely mathematical endeavors and also into other parts of his life (Krantz, 2001):

“When he played bridge at lunch with a group of friends, he would invariably say, every time he bid or played, "Did I do the right thing? Was that a good play? His partner Norman Levison, would patiently reassure him each time that he couldn't have done any better.”

- Excerpt, Mathematical Anecdotes by Stephen G. Krantz (1990)

Indeed, Wiener was notoriously insecure. According to Nasar (1998), he would ask anxiously if his name appeared in whatever books people were reading:

“At his low points, he fell prey to paralyzing depressions that drove him to threaten suicide frequently in the confines of his home and family, and at times among his MIT colleagues.” — Nasar (1998)

“When he became famous, he hounded his faculty colleagues to learn “what others at MIT thought of him.” When the talk turned to people at other institutions, “his first question was ‘What do they think of my work?’” — Conway & Siegelman (2005)

According to renowned Nobel Laureate economist Paul Samuelson (1915–2009), also of MIT, the lack of acceptance from Harvard did not help:

“The exodus from Harvard dealt a lasting psychic trauma to Norbert Wiener. It did not help that his father was a Harvard professor […] or that Norbert’s mother regarded his move as a cruel comedown in life” — Paul Samuelson, 1964

Wiener himself, perhaps not unsurprisingly, believed that “society’s understanding of mental illness could benefit greatly from the lessons afforded by the new brain-like computing machines” (Conway & Siegelman, 2005):

He suggested that many human "functional" (as opposed to organic) mental disorders were "fundamentally diseases of memory, of the circulating information kept by the brain in the active state"

[...] 

He explained how modern problems such as "malignant worry," anxiety attacks, and other classic neurotic disorders might start with a relatively trivial concern and "build itself up into a process totally destructive to the ordinary mental life," just as a computer caught up in a logical paradox "may go into a circular process which there seems to be no way to stop".

- Excerpt, Dark Hero of the Information Age by Conway & Siegelman (2005)

Personal Life

“We are not the stuff that abides, but patterns that perpetuate themselves.”

Wiener’s parents arranged his marriage in 1926, to a German immigrant named Margaret Engemann. Despite this circumstance, the two remained together for the rest of their lives, and had two children, Barbara and Margaret “Peggy”. They lived in Cambridge, Massachusetts. His insecurities, absent-mindedness and propensity for depression notwithstanding, by all accounts Wiener was a good father and a great friend:

“Wiener took his paternal responsibilities seriously, and in particular sought to avoid the pattern of education imposed on him by his father. In appraising him as a father, his alter-emotional life, which must have made him difficult, have to be balanced against his lively, imaginative companionship and his warm interest in the welfare of his daughters.”

- Excerpt, John von Neumann and Norbert Wiener by Steve J. Heims (1980)

In fact, stories of Wiener’s gentle and caring demeanor are many.

“Perhaps because of his own psychological struggles, Wiener had an acute empathy for other people’s trials. […] When a younger colleague was writing a book but couldn’t afford a typewriter, Wiener showed up at his door with a Royal portable under his arm.” — Nasar (1998)

The widow of his graduate student Norman Levinson described how in the fall of 1933, Wiener "arranged for Levinson to spend the next academic year in England studying higher mathematics, as he had, with G. H. Hardy at Cambridge", even caring for his parents when he was gone:

“Norbert Wiener went to the little working class slum where Norman’s parents lived to reassure them. The whole time Norman was in England, Norbert came to their house, usually on Saturdays, and he would talk to them, not about his theorems, but about nice, practical things, about England, landladies, tea time, high table”.— Fagi Levinson

Death (1964)

Norbert Wiener died on March 18th, 1964 of a heart attack in Stockholm, Sweden where he gave a lecture at the Royal Academy of Sciences. He was 69 years old. As the news reached MIT,

“Work came to a halt as people gathered to share the news and their memories, and the institute's flags were lowered to half staff in honour of the fallen institute professor who had roamed its halls for forty-five years.”

- Excerpt, Dark Hero of the Information Age by Conway & Siegelman (2005)

Those interested in reading more about the life of Norbert Wiener are encouraged to look up two books: Dark Hero of the Information Age* by Conway & Siegelman (2005) and Harmonies of Disorder* by Leone Montagnini (2017). 

References

• Chatterji, S.D. 1994. The Mathematical Work of Norbert Wiener (1894–1964). Kybernetes 26 (6/7). p. 34.
• Conway, F. & Siegelman, J. 2005. Dark Hero of the Information Age. Basic Books.
• Dyson, F. 2005. The Tragic Tale of a Genius. The New York Review of Books.
• Dyson, G. 2012. Turing’s Cathedral. Pantheon Books. New York, NY.
• Heims, S.J. 1980. John von Neumann and Norbert Wiener. The MIT Press.
• Kranz, S.G. 2001. Mathmatical Anecdotes in Mathematical Conversations: Selections from the Mathematical Intelligencer by Wilson & Gray. Springer-Verlag, New York, NY.
• Montagnini, L. 2017. Harmonies of Disorder. Springer.
• Nasar, S. 1998. A Beautiful Mind. Simon & Schuster.
• Wiener, N. 1953. Ex-prodigy. The MIT Press.

* This essay contains Amazon Affiliate Links