How many of us had problems remembering the values of sine and cosine for angles of 30 °, 60 °, and 45 °? Almost everyone faced problems and we were given various tricks to remember them. Wait, what about functions like the natural logarithm ( ln ) or e to the power x? What if we had a simple expression through which we could approximate the value of these non-polynomial functions?

I think Taylor Series is most useful in Physics. We can directly use them to approximate natural logarithms and sines.

That’s where the Taylor Series comes in. They are a series of so-called Taylor Polynomials. A polynomial is simply an expression which we can easily solve without the help of a scientific calculator instead,

Intuition

How can we make a polynomial which closely approximates the cosine function by assigning appropriate values for constants a₀, a₁, etc? Let’s take a look at the cosine function and for simplicity, we consider the first three terms of the general form of a polynomial.

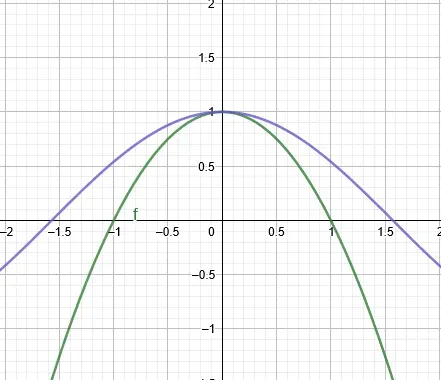
Note: In all the graphs, the red curve represents our polynomial function whereas the blue curve represents the cosine function.

Let’s play with the constants,

At x = 0, the value of cosine is 1. As you can see in the general formula if x equals 0 all the terms except a₀ are cancelled.

Let’s plug in the value of a₀ as 1. The general expression and its formula looks like this,

We have broadly approximated our polynomial function at x = 0. We will now make it more precise by finding an appropriate value for the constant a₁.

At x = 0 again, the slope of the tangent line on the cosine function is 0. Meaning, the first-order derivative of the cosine function with respect to x at x = 0 is 0.

We know,

Taking the derivative of our polynomial function with respect to x at x = 0, we make sure that this derivative matches the derivative of cosine at x = 0.

To have both the derivatives equal,

So, we have got value for a₁ too, which is equal to zero. Now, our polynomial function looks like,

Now, we need to match the second-order derivative of both the functions.

We now match the second-order derivative of the cosine function which that of our polynomial function. The second-order derivative could be thought of a the rate measurer of another rate measurer. This will increase the precision of our function.

The 2nd order derivative of our polynomial function and the cosine function is,

The value of the second derivative of cosine must be equal to the second-order derivative of our polynomial,

So we have a value of the constant a₂ which is -1/2. Our polynomial and its graph now looks like,

As you can see, more and the more the derivatives we take, the more approximate curve we obtain. We obtain two more derivatives of the polynomial and cosine functions. For this, we need to take more than three terms in our polynomial. After that, the polynomial looks like,

And its graph,

To compute higher-order derivatives likewise, we repetitively apply the power rule. Study the example,

We can match the derivatives with the derivatives of the same order of cosine function. In the end, we are arrive at,

Which indeed gives us the Taylor Series. Wikipedia says,

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function’s derivatives at a single point.

And,

The polynomial formed by taking some initial terms of the Taylor series is called a Taylor polynomial. The Taylor series of a function is the limit of that function’s Taylor polynomials as the degree increases, provided that the limit exists.

So, the Taylor series gives us a way to express non-polynomial functions like cosine, sine, eˣ in the form of a polynomial which we can compute. Like cosine, we have Taylor Series for sine and eˣ too.

The End

I know this wasn’t machine learning again! But mathematics has been my interest and I love to write on it. Thanks for reading and keep approximating!