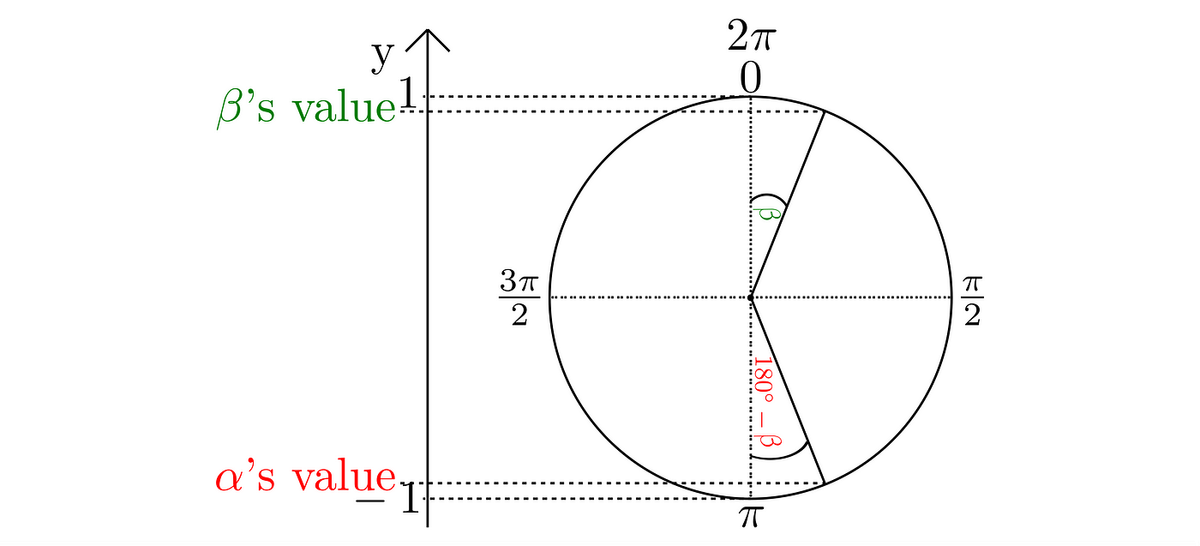
Everybody knows the angle of a straight line is 180°(π.) Yet, there would be no point in writing an article about it if that would be all. There must be something more, and, indeed, there is. Because every angle involves trigonometry within. They are like twins. And supplementary ones show quite interesting properties. Proving the law of sines for obtuse triangles? Better know them… or you are stuck. So, what is it all about? Let us go find out.

By way of introduction, we are going to work with a straight angle separated into α and β, like so:

which must add up to 180°, that is:

Of course, if one of them is known, then the second is explicitly determined too.

Keep it in mind that α and β do not need to be situated on a straight line. All the following reasoning concerns any two angles that together are 180°. They could be separated, defined in different figures, even disunited by the whole universe, as long as they add up to 180°, all will hold.

The sine identity

Since a straight angle is equal to 180°(π), the α and β have to be defined in <0,π> range. So, let us mark α somewhere on our plot, for example:

And raise the question about the value of β, what is it? Well, we know the answer: β=180°-α. Thus, imagine subtracting α from π. Since the sine function is symmetrical, the value of β will be the same as for α. Just take a look:

Hence:

This identity could also be shown with a unite circle, as follows:

The cosine identity

Even though the function changed into the cosine, the angles are still in <0, π> range because we deal with the same one which is 180°. The cosine values various from 1 to -1 in there. The question is what relationship between our angles is now. So, again, let us start by choosing α somewhere on that plot.

And now, we could get β by subtracting α from π.

Since adding β to α make π and because of symmetry of the cosine function, its values for any two angles that sum to 180° must be opposite to each other; therefore:

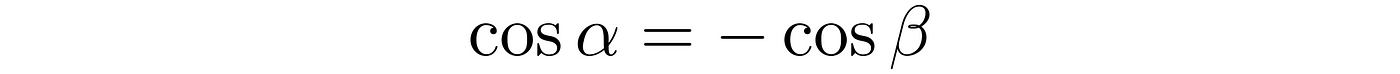
Similarly to sine, it could be shown with a unite circle whose radians are properly adjusted to the cosine function.