On August 2. 2020 Cantor’s Paradise published Bruno Campello’s brief critique of Cantor’s approach in transfinite mathematics. The author raises some doubts about Cantor’s debunking Euclid’s 5th principle stating that the whole is greater than the part. Campello gives an interesting argument against Cantor’s reasoning, but it itself raises a number of question marks to say the least. Below I comment on his discussion of the alleged Cantor’s fallacy.

Georg Cantor RefutedThe celebrated Georg Cantor believed he could refute Euclid’s 5th principle (that the whole is greater than the part)…medium.com

To begin with, Campello says that “Cantor and his epigones believed that, along with a principle of ancient geometry, he was also breaking down an established belief of common sense and one of the pillars of classical logic”, but it seems that not only Cantor and his mob believed it — the article comes to a close with these words:

That such crude sophisms could pass as serious threats to the foundations of classical geometry and even to the principles of civilization that we inherited from the Greco-Roman tradition, is only the sign of the impotent revolt of the mathematical imagination exacerbated against the real order of things

Wherein the reality of this change is acknowledged by the author. However, regardless of his opinion about this shift, it must be clarified that it was not Cantor who originated the disbelief in common sense in scientific reasoning that “demolished our civilisation”.

In fact, the revolution Campello dispises so much took place a long time before Cantor. It was Newton and Galileo who were first to decide to entrust the scientific explanation to their abstract mathematical models at the price of intuitive intelligibility coming from common sense and observation. After them, science strives for consistent theory of a mere fragment of phenomena, even if the theory contradicts some other aspects of reality (Chomsky, Belletti, Rizzi, 1999, p. 3). Steven Weinberg called this kind of making science the “Galilean style” (Weinberg, 1976, pp. 28–29). It stems from the “recognition that it is the abstract systems that you are constructing that are really the truth; the array of phenomena are some distortion of the truth” (Chomsky, Belletti, Rizzi, 1999). And indeed, today’s science bases securely on the mathematical imagination, rather than on the common sense. The latter, it seems, died with the Middle Ages.

So it is not Cantor who is responsible for “crude sophisms” in science, but the very fathers of the modern science. That’s for starters. But let us turn to the heart of Campello’s critique now, and see where he believes Cantor went wrong.

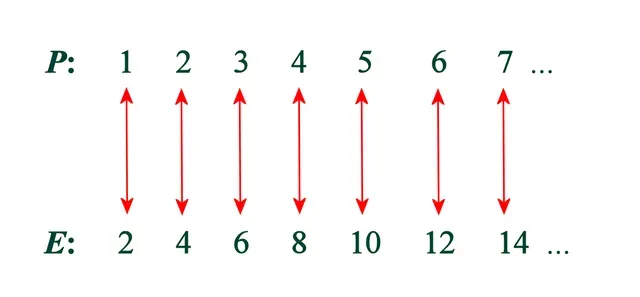
Entire issue here is Cantor’s striking conclusion that if we are to compare two infinities, namely the infinite set of integers and the infinite set of even numbers, we can put their elements in one-to-one correspondence, hence both sets are equinumerous. This is to break Euclid’s 5th principle, as the evens are a subset of integers. Such result was indeed staggering and raised eyebrows of many leading mathematicians of the era, including Kronecker, Weierstraß, and the proto-intuitionist Poincaré. But now Campello has a decisive argument against it, so we can relax. What is this argument?

Firstly, Campello explains that one can treat infinity as an object that can be a subject to arithmetical operations and comparisons only if one takes it to be the actual infinity, that could be thought of as a unity. And this of course deends on one’s philosophical standpoint. If one does not allow for such treatment and only understands infinity as potential, that is, something which is never a finished whole, but rather which could be always (potentially) increased, Cantor’s approach will be unjustified from the beginning.

The discussion about the nature of infinity is maybe one of the most absorbing in philosophy of mathematics, and that is likely because of the lack of decisive results. Any argument against the notion of the actual infinity I have heard of could be parried by the Platonist Cantor. For instance, the Kantian claim that the infinite is never experienced in nature, hence can be only conceived as a potential entity, meets the answer that the nature of mathematical endeavour exceeds the matter of experience and sensual observation, so its principles go beyond the physical and there is no immediate contradiction in the notion of actual infinity. In fact, the most convincing reservation I have encountered is simply that the concept of the actual infinite goes directly against common sense and is thus unintelligible. But we have seen that arguments “from common sense” do not work here.

Yet Campello does not try to discuss the fact that the actual/potential issue is the matter of philosophy of mathematics, and merely refers to Aristotle’s authority. He knows that this ab auctoritate would not suffice to knock Cantor down, so he goes on with his argument.

It starts with a scrupulous distinction between a sign standing for a number and the number itself. Campello believes that Cantor’s mistake is caused by confusion of these two:

If we represent the whole numbers each by a sign (or cipher), we will have there an (infinite) set of signs or ciphers; and if, in this set, we want to highlight the numbers that represent pairs by special signs or numbers, then we will have a “second” set that will be part of the first; and, both being infinite, the two sets will have the same number of elements, confirming Cantor’s argument. But that is to confuse numbers with their mere signs […].

He continues: “ it is not the sign “4” which is twice as much as 2, but the quantity 4, whether it is represented by this sign or by four little balls”. This latter sentence I take to express the essence of Campello’s demonstration. It sounds reasonable. But there is a lot more behind this approach than mere common sense. As a matter of fact, Campello’s reasoning presupposes a particular notion of number, and this being not free of philosophical shortcomings.

The concept of number Campello sympathizes with originates from Husserl’s early work in philosophy of mathematics, Philosophie der Arithmetik. “In the first part of the work, Husserl developed a psychological analysis that started from the everyday concept of a number” (Beduerftig & Murawski, 2018, p. 36) — something Campello is surely fond of for its commonsensicality. In his oeuvre, Husserl builds the general concept of number in a strictly epistemological way: he takes the notion of number to be the abstraction of quantitative features of the perceptible phenomena, which is made by the intellect. Firstly, he notes that while perceiving the world, we encounter various appearances. To distinguish them from each other, we use the relations of “difference” and “identity” (Husserl, 2003, p. 52). Our mental faculty allows us to spot that things we see are not all one, but are different. They differ in terms of their identity — A differs from B, B differs from C, etc. (Husserl, 2003, p. 53). In other words, we have one thing (different from any other), than another, and so on.Then we abstract the one-ness of things into the concept of unity, i. e. number one. And in order to arrive at bigger numbers, be simply add them together:

“One and one, … , and one — a form with which a definite number term is associated” (Husserl, 2003, p.86).

“Unity” is here understood simply as the number one, and this is the “unity” which makes 2 twice as much as 1, as Campello would put it.

And so, he says that the “set of whole numbers may contain more numerical signs than the set of even numbers — since it includes both odd and even signs — but not a greater number of units than that contained in the even series.” His entire analysis depends heavily on this “quantitative” understanding of a number and recognizing units as bricks making up the structure of numbers. Now it is obvious why he accepts only the potential infinite.

Later on in the article, Campello accuses Cantor of metaphysical speculation, but now it seems that it is not only Cantor who is eager to assert positive claims about mathematical reality: the author himself, consciously or not, relies heavily on some philosophical interpretation of numbers and infinity. Moreover, his accusation against the refutation of the 5th principle that “[Cantor’s reasoning] is obviously metaphysical, since it aims not only to imagine a possible space but to describe a property of real space” makes entire mathematical practice a metaphysical endeavor.

But it is even worse than that. Campello openly imposes his philosophical standpoint on Cantor, and then criticizes him for not playing by the inflicted rules. However, it is the difference in philosophical accounts between Cantor and the author that causes the issue, not the confusion of sign and number. To see that, let us take a brief look at Cantor’s conception of number, one that lets him not only talk about the actual infinite, but also compare it with other objects of the system.

His approach is more abstract from the beginning. The key term in Cantor’s ontology is a set, and his account hinges strongly on it. But it does not need as refined an explanation as the Husserlian stnace: a number is defined on the basis of equinumerosity of sets (that idea is actually due to Frege). The general concept of a number is understood as the intersection of all sets with the same number of elements. What makes this intersection possible is the property of “having n elements”. This approach does not focus on the quantitative feature; it’s idea is that as long as some elements can compose a set, it does not matter how many of them is there — even if infinitely many.

What follows from it is that a number for Cantor is not a structure of units, but a complete unity of a set. Crazy as it sounds, being a set is more important than the number of elements a set has. Hence, what is crucial in the number “2” is that it is an intersection of sets; what is crucial in “4” is also that it is an intersection of sets. There is nothing twice as many in 4 as in 2, because they are only two different sets.

Understood in this way, numbers do not “differ in size”, as Campello would probably like to state it. They are entities of the same kind, perfectly camparable to one another. We find out that on this account, if we look for sets equinumerous with the set of integers, we will come by the set of even numbers, since it is possible to establish an isomorphism between them. Thus they are the same kind of infinity. So Cantor rejoins (when judged by his standards, as he should have been).

If Campello wanted to effectively attack Cantor’s idea, he should have gone for the root of it, the meta-mathematical assumption that Cantor makes for his transfinite arithmetic. Instead, he chose to aim at the problem that arises only in his own defective interpretation of Cantor, an interpretation unaware of its own philosophical weight. Campello’s refolmulation only brought unclarity. Add to that vague accusations about metaphysical nature of Cantor’s business and you don’t know which confusion should be rectified first.

I believe that we can learn two things on this account. First, that if geniuses of first order like Poincaré or Brouwer were not able to effectively demolish Cantor’s set-theoretical approach, there probably is some point to it. Second, that while entering the discussion in the philosophy of mathematics, one should know the root of the discussed issue, since the prima facie diagnosis could not suffice. As Sir Arthur Eddington said:

We used to think that if we knew one, we knew two, because one and one are two. We are finding that we must learn a great deal more about ‘and.’

Reading LIst

1. Chomsky, Belletti & Rizzi (1999). “An Interview on Minimalism”, University of Siena, Nov 8–9 (rev: March 16, 2000) .
2. Weinberg (1976). “The forces of nature”, Bulletin of the American Society of Arts and Sciences 29.4.
3. Beruerfrig & Murawski (2018). “Phenomenological Ideas in the Philosophy of Mathematics from Husserl to Gödel”, Studia semiotyczne, XXXII, No. 2 (2018), 33–50.
4. Husserl (2003). Philosophy of Arithmetic, trans. D.Willard, Dordrecht: Springer Science+Business Media.