Ramanujan

Ramanujan’s Early Work on Continued Fractions

Jørgen Veisdal

— 12 min read
Ramanujan’s Early Work on Continued Fractions
“I had never seen anything in the least like [it] before” — G.H. Hardy

On or about the 31st of January 1913, mathematician G.H. Hardy (1877-1947) of Trinity College at Cambridge University received a parcel of papers from Madras, India. The package included a cover letter where a young clerk by the name of Srinivasa Ramanujan (1887–1920) provided an introduction of himself and his precarious situation, as well as various mathematical claims about the domain of the gamma function and the distribution of prime numbers. 

This essay provides a narration of Ramanujan and Hardy’s subsequent correspondence on the topic of continued fractions, in addition to an overview of the fractions Ramanujan claimed to have discovered, and their history. The essay is based in large part on the wonderful book Ramanujan: Letters and Commentary* by Berndt & Rankin (1991).

Hardy’s First Letter (February 8th)

G. H. Hardy replied to Ramanujan’s letter on the 8th of February 1913. His response begins by recognizing his excitement for the contents of Ramanujan’s first letter:

Dear Sir. I was exceedingly interested by your letter and by the theorems which you state

Having shown Ramanujan’s letter to J. E. Littlewood (1885–1977) (who was immediately amazed by Ramanujan’s genius) Hardy concluded for himself that the young Indian mathematician was indeed “a mathematician of the highest quality, a man of altogether exceptional originality and power”. In his response letter, Hardy however goes on to state:

You will however understand that, before I can judge properly of the value of what you have done, it is essential that I should see proofs of some of your assertions.

That is, Hardy wants Ramanujan to send him mathematical proofs of his claims, in particular, he is interested in his theorem on continued fractions. As Hardy writes “almost everything depends on the precise rigour of the methods of proof which you have used”. Lacking proofs, Hardy goes on to classify the assertions in Ramanujan’s letter as follows:

Your results seem to me to fall into roughly 3 classes:

(1) There are a number of results which are already known, or are easily deducible from known theorems;

(2) There are results which, so far as I know, are new and interesting but interesting rather from their curiosity and apparent difficulty than their importance;

(3) There are results which appear new and important, but in which almost everything depends on the precise rigour of the methods of proof which you have used.

After categorizing Ramanujan’s various claims, Hardy ends his letter:

I hope very much that you will send me as quickly as possible at any rate a few of your proofs, and follow this more at your leisure by a more detailed account of your work on primes and divergent series. 

It seems to be quite likely that you have done a great deal of work worth publication; and, if you can produce satisfactory demonstrations, I should be very glad to do what I can to secure it.

[...]

Hoping to hear from you again as soon as possible.

I am
Yours very truly,
G.H. Hardy

Ramanujan’s Second Letter (27th of February)

Dear Sir

I am very much gratified on perusing your letter of the 8th February 1913. I was expecting a reply from you similar to one which a Mathematics Professor at London wrote asking me to study carefully Bromwich's Infinite Series and not fall into the pitfalls of divergent series.

Ramanujan is referring to a response he received from M. J. M. Hill (1856–1929) of the University College London (UCL) around the same time as his first correspondence with Hardy. Upon reviewing Ramanujan’s work, Hill had commented that his papers were “riddled with holes” and that although Ramanujan had “a taste for mathematics, and some ability”, he lacked the necessary educational background to be accepted by the mathematical community (Kanigel, 1991).

Ramanujan thus no doubt was encouraged by Hardy’s reply. He goes on to describe a procedure which he believes will assure Hardy of the truth of his claims (without in fact sending him the proofs):

I have found a friend in you who views my labours sympathetically. This is already some encouragement to me to proceed with my onward course. I find in many a place in your letter rigorous proofs are required and so on and you ask me to communicate the methods of proof. If I had given you my methods of proof I am sure you will follow the London Professor. But as a fact I did not give him any proof but made some assertions as the following under my new theory.

Since he lacked formal training in higher mathematics, Ramanujan was understandably worried that any proofs he was able formulate (and communicate) might be incorrect and/or insufficiently rigorous — risking losing Hardy’s interest:

If I tell you this you will at once point out to me the lunatic asylum as my goal. I dilate on this simply to convince you that you will not be able to follow my methods of proof if I indicate the lines on which I proceed in a single letter.

Rather than send proofs, Ramanujan instead proposes a procedure by which he hopes Hardy would be able to verify his results:

You may ask how you can accept results based upon wrong premises. What I tell you is this. Verify the results I give and if they agree with your results, got by treading on the groove in which the present day mathematicians move, you should at least grant that there may be some truths in my fundamental basis.

Ramanujan next goes on to express that, before being able to work on proving his claims, his first priority is to obtain a scholarship or fellowship from the Indian government in order to secure his himself from starvation. A few months later, Madras University granted Ramanujan a monthly scholarship of £5 for two years, approximately $130 adjusted for inflation.

You may judge me hard that I am silent on the methods of proof. I have to re-iterate that I may be misunderstood if I give in a short compass the lines on which I proceed. It is not on account of my unwillingness on my part but because I fear I shall not be able to explain everything in a letter.

I do not mean that the methods should be buried with me. I shall have them published if my results are recognised by eminent men like you.

Ramanujan moves on to address Hardy’s response to some of the mathematics of Ramanujan’s claims about the distribution of prime numbers. His second letter was sent on the 27th of February 1913.

Hardy’s Second Response Letter (26th of March)

G. H. Hardy responded to Ramanujan’s second letter on the 26th of March 1913. He begins:

Dear Mr Ramanujan,
Since I wrote to you last I have heard from Mr Littlewood to whom I sent your last letter to me, and I have considered further some of your results.

Littlewood — whose specialty was number theory — was exceedingly impressed and excited by Ramanujan’s claims, perhaps even more so than Hardy himself, writing to Hardy in early March that

“I can believe he’s at least a Jacobi” — J.E. Littlewood (1913)

Hardy’s letter to Ramanujan goes on to speculate about why — other than his abilities — Ramanujan might be unwilling to communicate proofs in his first two letters:

Mr Littlewood suggested to me also that your unwillingness to give proofs was probably due to apprehensions as to the use I might make of your results. Let me put the matter quite plainly to you. You have in your possession now 3 long letters of mine, in which I speak quite plainly about what you have proved or claim to be able to prove. I have shown your letters to Mr Littlewood, Dr Barnes, Mr Berry, and other mathematicians.

Surely it is obvious that, if I were to attempt to make any illegitimate use of your results, nothing would be easier for you than to expose me.

Seemingly true, yes. However, one can certainly think of easier things than for a clerk in Madras, India in 1913 to successfully discredit a Cambridge Fellow across the globe with three hand-written letters discussing highly complex mathematics. Hardy however goes on:

You will, I am sure, excuse my stating the case with such bluntness: I should not do so if I were not genuinely anxious to see what can be done to give you a better chance of making the best use of your obvious mathematical gifts.

Hardy goes on to write that what he most wants Ramanujan to provide is a proof of his claims “concerning continued fractions of the type”:

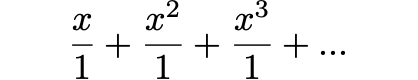
He ends his second letter to Ramanujan:

I am quite sure that the wisest thing you can do, in your own interests, is to let me have one as soon as possible.

I am, Yours very sincerely
G. H. Hardy.

Ramanujan’s Third Letter (17th of April)

Ramanujan replies to Hardy’s second letter on the 17th of April, 1913. He again ignores Hardy’s request for a proof of his claims about continued fractions, instead trying to address his claims about the distribution of prime numbers (which ultimately turn out to be incorrect).

Ramanujan’s Early Work on Continued Fractions

Definition of a Continued Fraction. A continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on.

As his second letter makes clear, G. H. Hardy was particularly impressed by Ramanujan’s findings on continued fractions, writing that his theorems “defeated me completely; I had never seen anything in the least like them before”, adding that they:

“Must be true, because, if they were not true, no one would have the imagination to invent them”. — G. H. Hardy, 1913

Ramanujan’s work on continued fractions appear in section “IX. Theorems on continued fractions” of his first letter. In total, he provides seven theorems related to continued fractions, all without proof.

Ramanujan’s First Continued Fraction

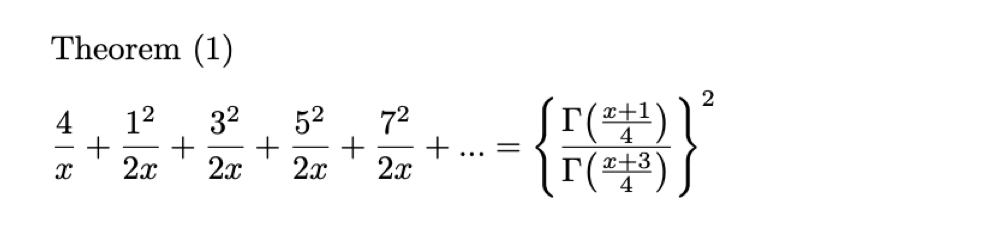
Ramanujan’s first continued fraction is Corollary 1 from Section 25, Chapter 12 in Ramanujan’s second notebook, a special case of a much more general theorem (Entry 39, Chapter 12). The theorem is due to a 1872 result by Gustav Conrad Bauer (1820–1906) included in the work:

Setting in for x = 1 obtains Lord William Brouncker (1620–1684)’s formula / continued fraction for estimating the value of pi:

For more on this formula, Berndt & Rankin (1991) recommend J. Dutka’s 1982 paper “Wallis’s Product, Brouncker’s Continued Fraction, and Leibniz’s Series” in Archive for History of Exact Sciences 26 pp. 115–126.

Another of Ramanujan’s results from his first paper was also previously proved by Bauer, namely theorem 3 in section “V. Theorems on summation of series”:

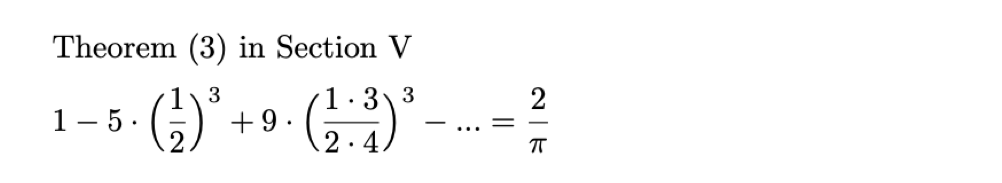
This was first shown by Bauer in the 1859 paper:

Ramanujan’s Second Continued Fraction

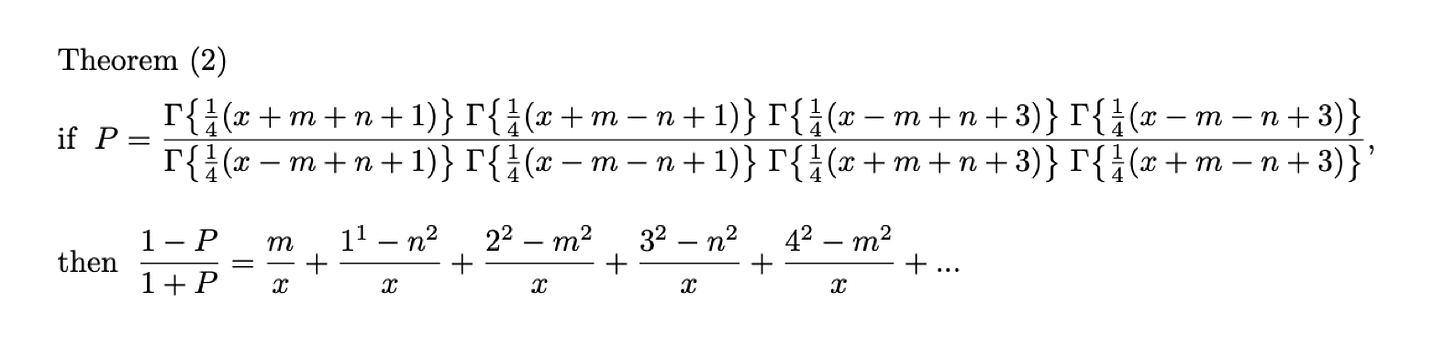
Theorem 2 in Section IX of Ramanujan’s first letter to G.H. Hardy (1913)

Ramanujan’s second continued fraction is Entry 34 in Chapter 12 of his second notebook. He never proved it himself, indeed the theorem was not until Preece published a proof 18 years later, in:

A different proof was later provided by Perron in the book:

  • Perron, O. (1957). Die Lehre von den Kettenbrüchen. Band II. B. G. Teubner, Stuttgart. pp. 34.

Berndt & Rankin (1991) also mentions later proofs by Liang-Cheng Zhang based on generalized hypergeometric series and by Lisa Lorentzen (formerly Jacobsen) showing that the theorem is valid provided that either 1. n is an odd integer; 2. m is an even integer or that the real value of x is greater than zero, Re(x) > 0, for m and n arbitrary complex numbers:

Ramanujan’s Third Continued Fraction

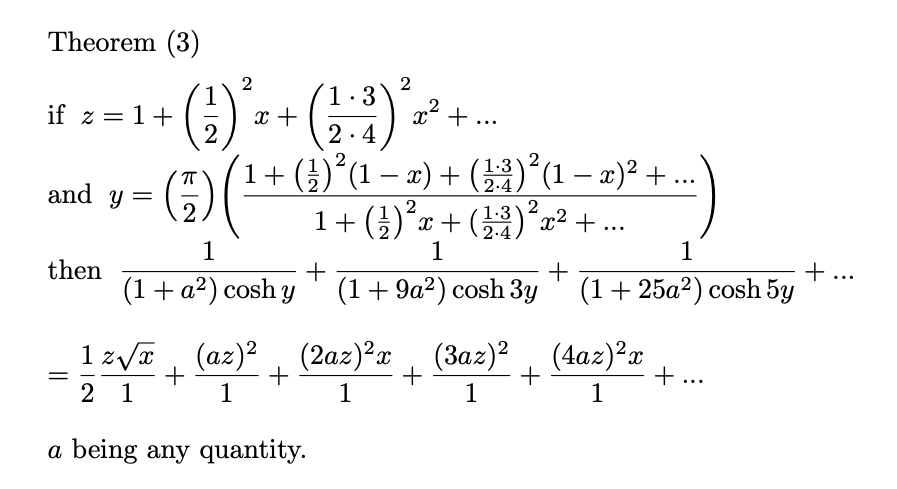
Theorem 3 in Section IX of Ramanujan’s first letter to G.H. Hardy (1913)

Ramanujan’s third continued fraction is Entry 12 in Chapter 18 of his second notebook. The formula is valid for 0 < x < 1 and a > 0.

Ramanujan’s Fourth Continued Fraction

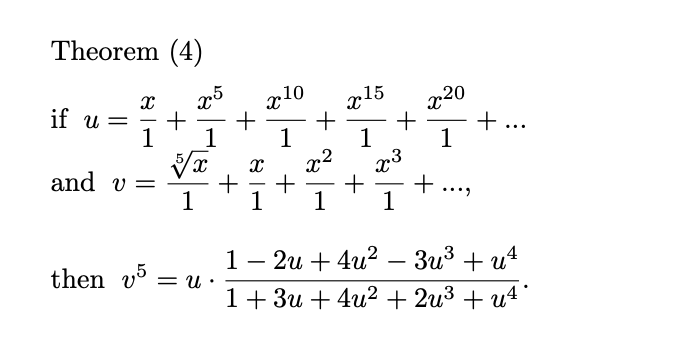
Theorem 4in Section IX of Ramanujan’s first letter to G.H. Hardy (1913)

In his first letter of response to Ramanujan, Hardy ranks his fourth continued fraction as a result which appears “new and important, but in which almost everything depends on the precise rigour of the methods of proof which you have used”. The fraction appears on page 289 in Ramanujan’s Second Notebook. Although Ramanujan himself once again had no proof of the claim, it was later proved by Leonard J. Rogers (1862–1933) in:

George Neville Watson (1886–1965) later provided another proof, published in:

Berndt & Rankin (1991) speculate that in addition to his work on continued fractions, the missing page of Ramanujan’s first letter to G.H. Hardy contained what would later known as the Rogers-Ramanujan identities. The two identities — related to hypergeometric series and integer partitions — were first discovered by Rogers in 1894, and then rediscovered without proof by Ramanujan, and sent to Hardy in his first letter. While looking for a proof of the relations, in 1917 Ramanujan discovered Rogers’ 1894 paper and the two published a joint new proof in 1919:

The Rogers-Ramanujan identities are closely related to the Rogers-Ramanujan continued fraction. Kollagunta G. Ramanathan (1920–1992) later developed the theorem further in:

More about the Rogers-Ramanujan continued fraction can be found in:

Ramanujan’s Fifth and Sixth Continued Fraction

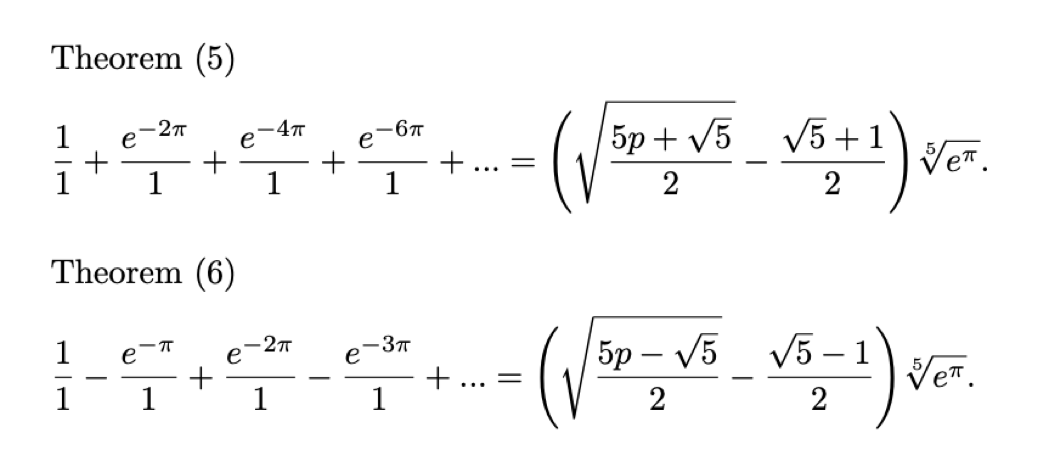
Theorems 5 and 6 in Section IX of Ramanujan’s first letter to G.H. Hardy (1913)

Both the fifth and sixth continued fraction Ramanujan provides in his first letter to G.H. Hardy are contained in Section 39, Chapter 16 of his second notebook. The theorems were first proved by George Neville Watson (1886–1965) in:

The relations were further developed by Ramanathan in:

Ramanujan’s Fifth and Sixth Continued Fraction

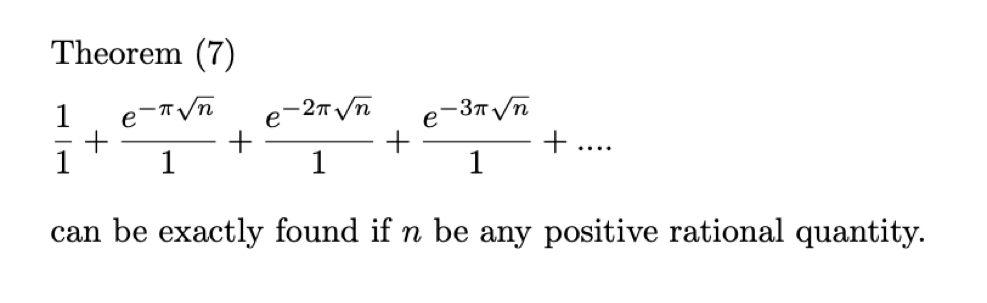
Theorem 7 in Section IX of Ramanujan’s first letter to G.H. Hardy (1913)

The last continued fraction Ramanujan sent Hardy in his first letter was also first proved by Watson, in:

This essay is based largely on the marvelous work Ramanujan: Letters and Commentary* by Berndt & Rankin (1991). I highly recommend anyone interested in the topics of Ramanujan, Hardy and Littlewood to buy this book, as this essay is in no way a substitution for the full work (which encompasses over 300 pages of correspondence, including detailed discussion and analysis).

Read more