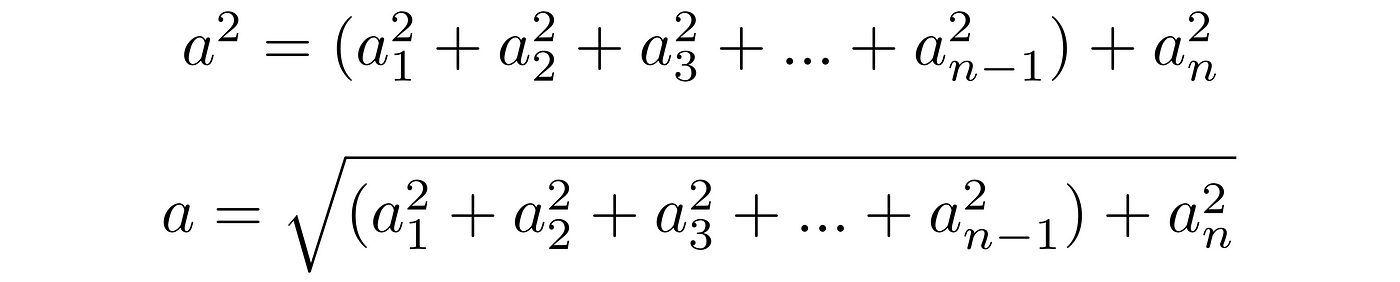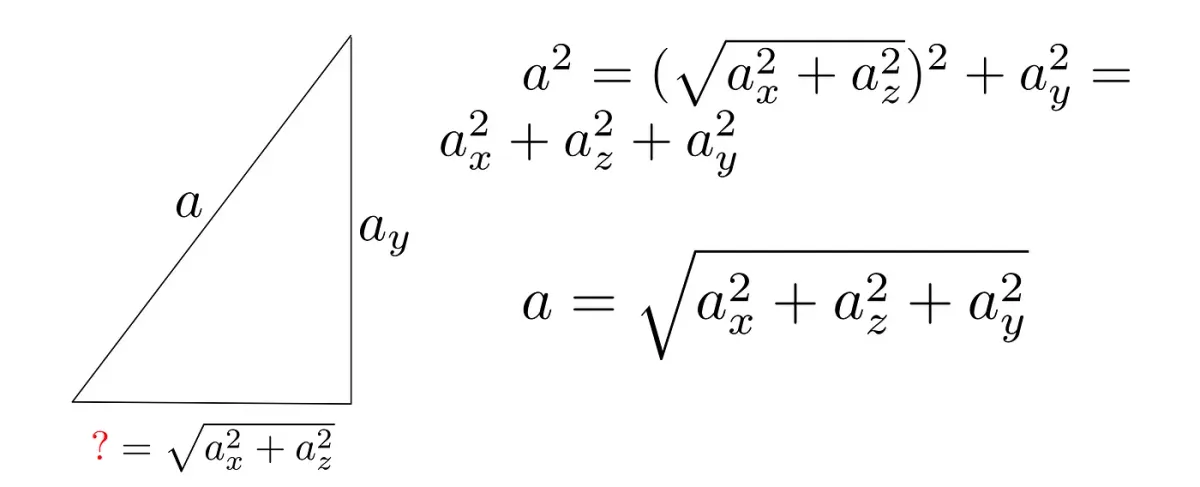
Pythagoras’ theorem provides the relationship between the sides of a right-angled triangle: the sum of the squares of the lengths of two sides equals the square of the hypotenuse.

It is one of these primaries theorem of all science. Just to say about vector notation as being involved in everything. Classical mechanics, electromagnetism, relativity, quantum mechanics are all benefits. If that so, it is good to not only know how to use it but also why it holds.

For that purpose, assume we have a sector divided at any point into two smaller pieces, called a and b, which are catheti of a right triangle.

Next, we need to add the hypotenuse, but to draw it, we have to move into 2D. So we treat the sector a+b as the length of the side of a square.

We additionally know that the area of a square is its side times side. In our case:

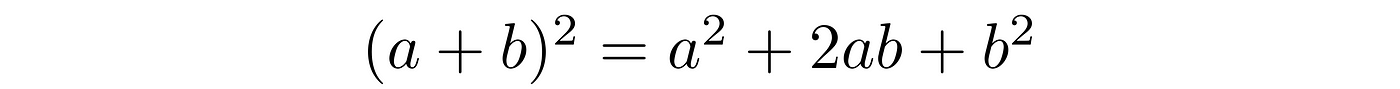
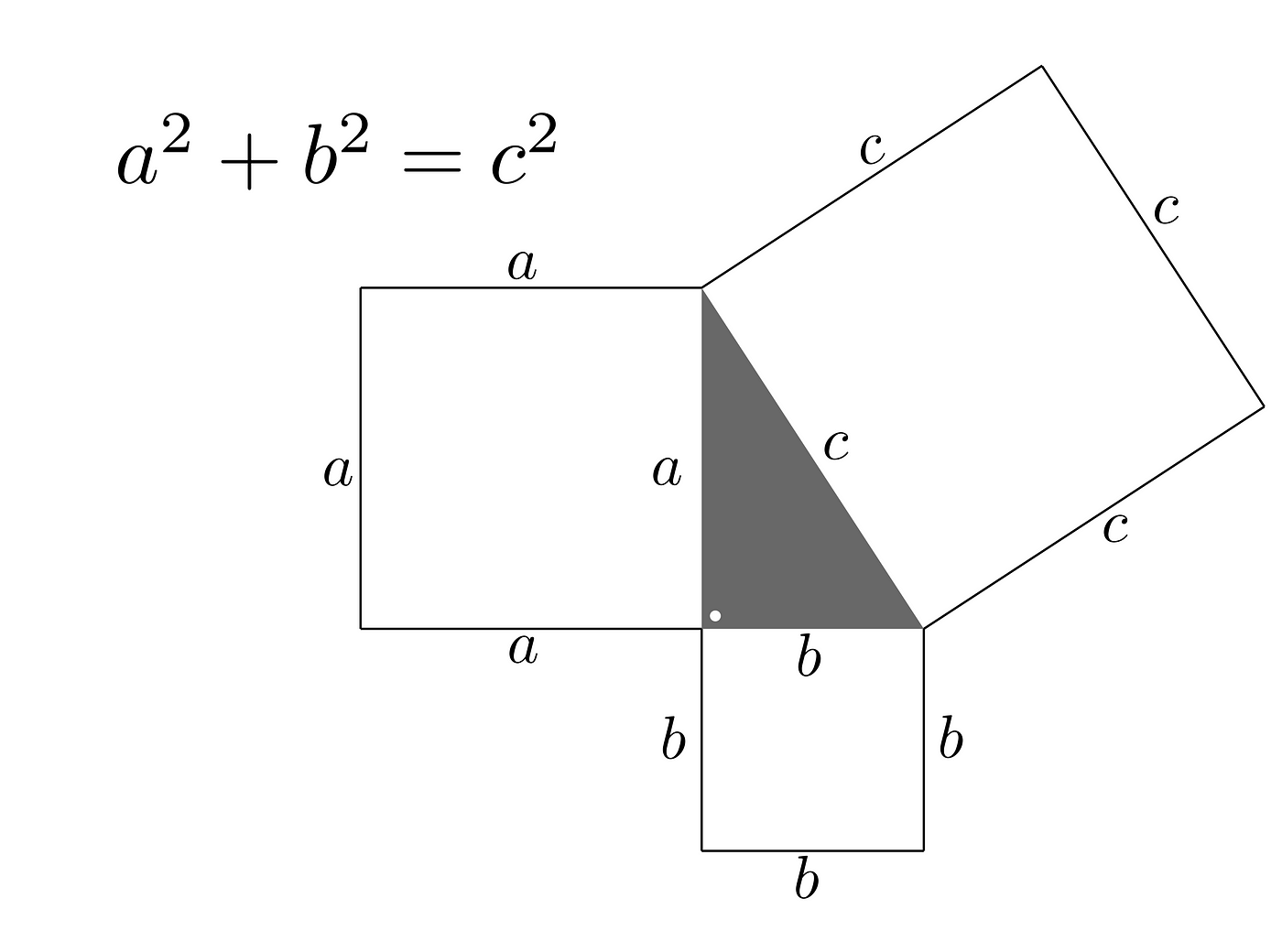
Now let’s form our triangle by cutting this area into smaller parts as follows:

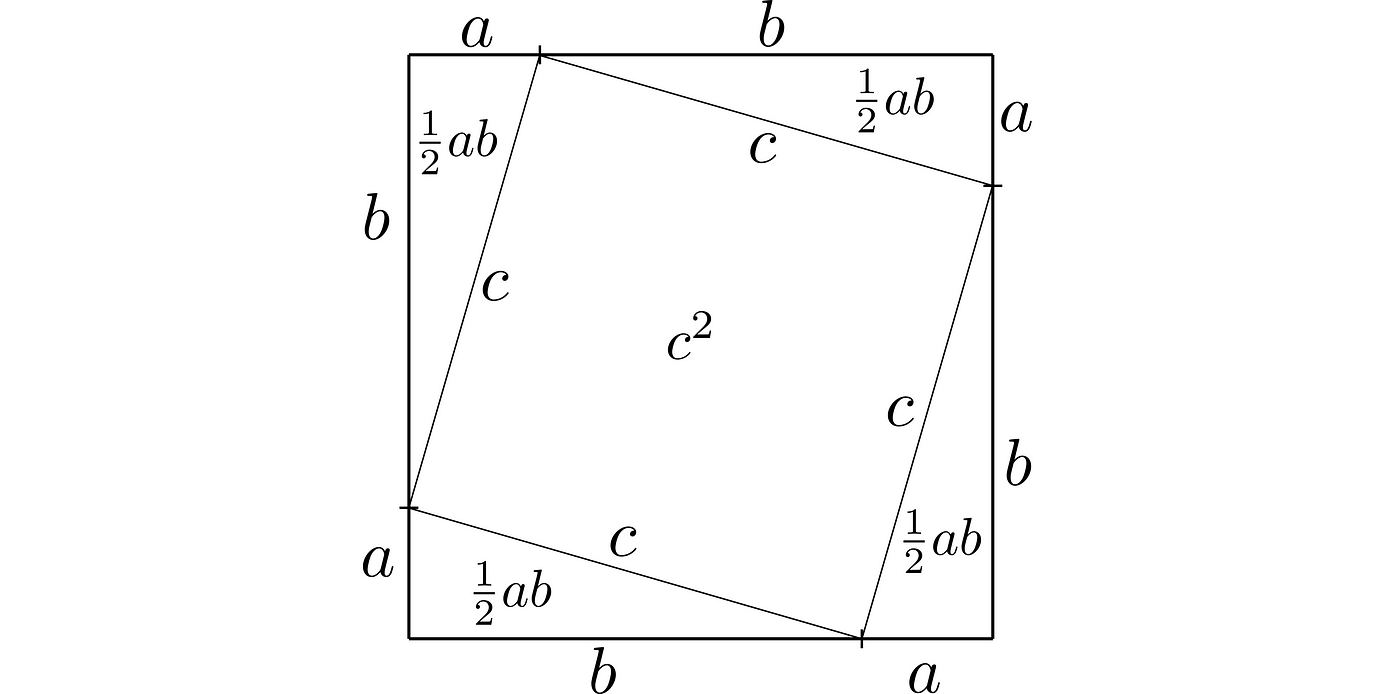
What we got are four identical right triangles of sides: a, b, c, and one square, which has side c. Their total area is equal to:

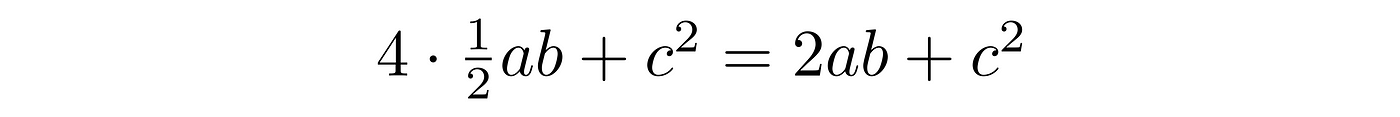
We fulfill the whole area of the initial square while forming them; thereby their total area has to be equal to the area of the square.

What profs the validity of the Pythagoras’ theorem.

But what about higher dimensions?

To understand how this two-dimensional case could be generalized in higher dimensions, let’s discuss the similar problem in 3D.

A coordinate system and a vector are what we need. Let’s draw some then.

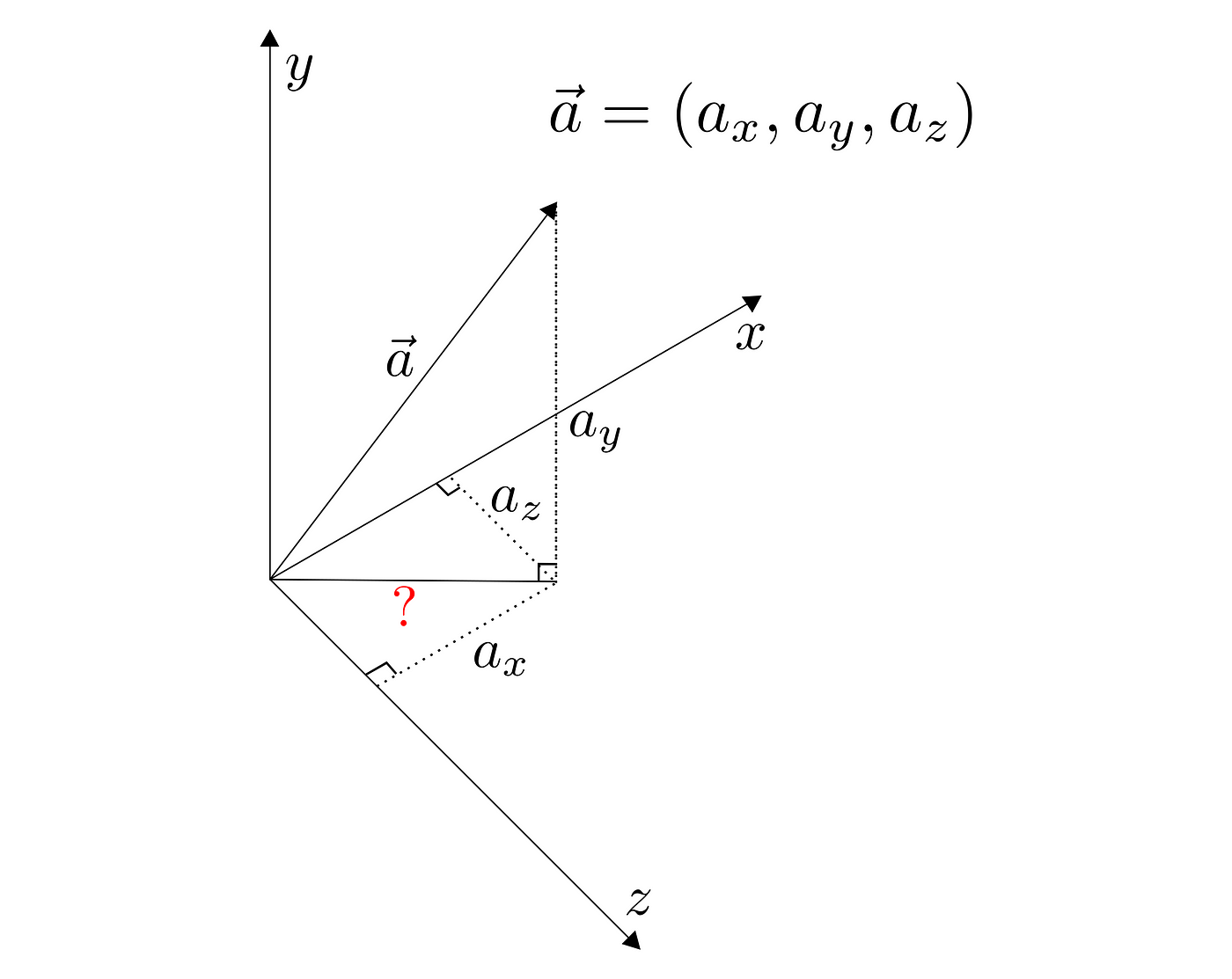
What is required to calculate the length of the a-vector is to find a right triangle that will allow us to use the formula. Notice then, that projection of any vector component is always perpendicular to the plane it crosses, and any of theirs pair is intersecting at right angle: that is because every axis is perpendicular to the others.

What does it mean for us?

The y-component, which extended our 2D space into the 3rd dimension, is perpendicular to the xz-plane. Then, if we only would know, what is the magnitude of the vector from the origin to the point where it crosses this plane, we would have our triangle and could use the formula.

So, what could it be?

Notice the x and z-components, as we said, are intersecting at right angle. Thus, if considering them as shown in the picture, they would form the rectangle whose diagonal is the vector that shares components along xz-plane with our a-vector, dividing it into two right triangles. Hence we could use the Pythagoras’ theorem to find its magnitude. That is:

And we have both sides of our right triangle now. The first one we just delivered and the second is the y-component itself.

Similar steps occur with even higher dimensions too. Having n-dimensional space, and struggling with determining the magnitude of a vector there, you could also divide it into two parts. The first one composed of n-1 dimensions will let you calculate the diagonal of the hyperrectangle, which would be the first side of the wanted right triangle. What is left from n dimensions, when we already took n-1 of it? This single one provides the nth-dimension by being the second side of the right triangle. Pulling out the essence: regardless of how many dimensions your coordinate system has, the theorem could be applied, always.

The formula for higher dimensions would then looks like this: