Ptolemy was an ancient astronomer, geographer, and mathematician who lived from (c. AD 100 — c. 170). He is most famous for proposing the model of the “Ptolemaic system”, where the Earth was considered the center of the universe, and the stars revolve around it. This was the generally accepted view for many centuries, until Copernicus (19 February 1473–24 May 1543) proposed the theory where the sun was the center with earth an other planets revolving around it.

Although, Ptolemy’s most famous idea turned out to be wrong, he did a lot of really useful work in geometry and we are going to discuss one of those very nice ideas.

Ptolemy’s Inequality

The statement of Ptolemy’s inequality is

You might have seen a similar version for triangles, which is called the triangle inequality. Let us now see how to prove this.

The Proof

Although, the proof here is easy to follow and self contained, the methods used are inspired from another article, where we have discussed the case of equality, instead of inequality. So, I recommend you to go through that one as well.

Let us start by drawing a diagram which contains 4 points in the plane as the vertices of a quadrilateral ABCD.

Now, we make a construction by marking two points X and Y on each of the diagonals respectively, such that ∠ BAX = ∠ CAD and ∠ ABY = ∠ ACD (diagram below).

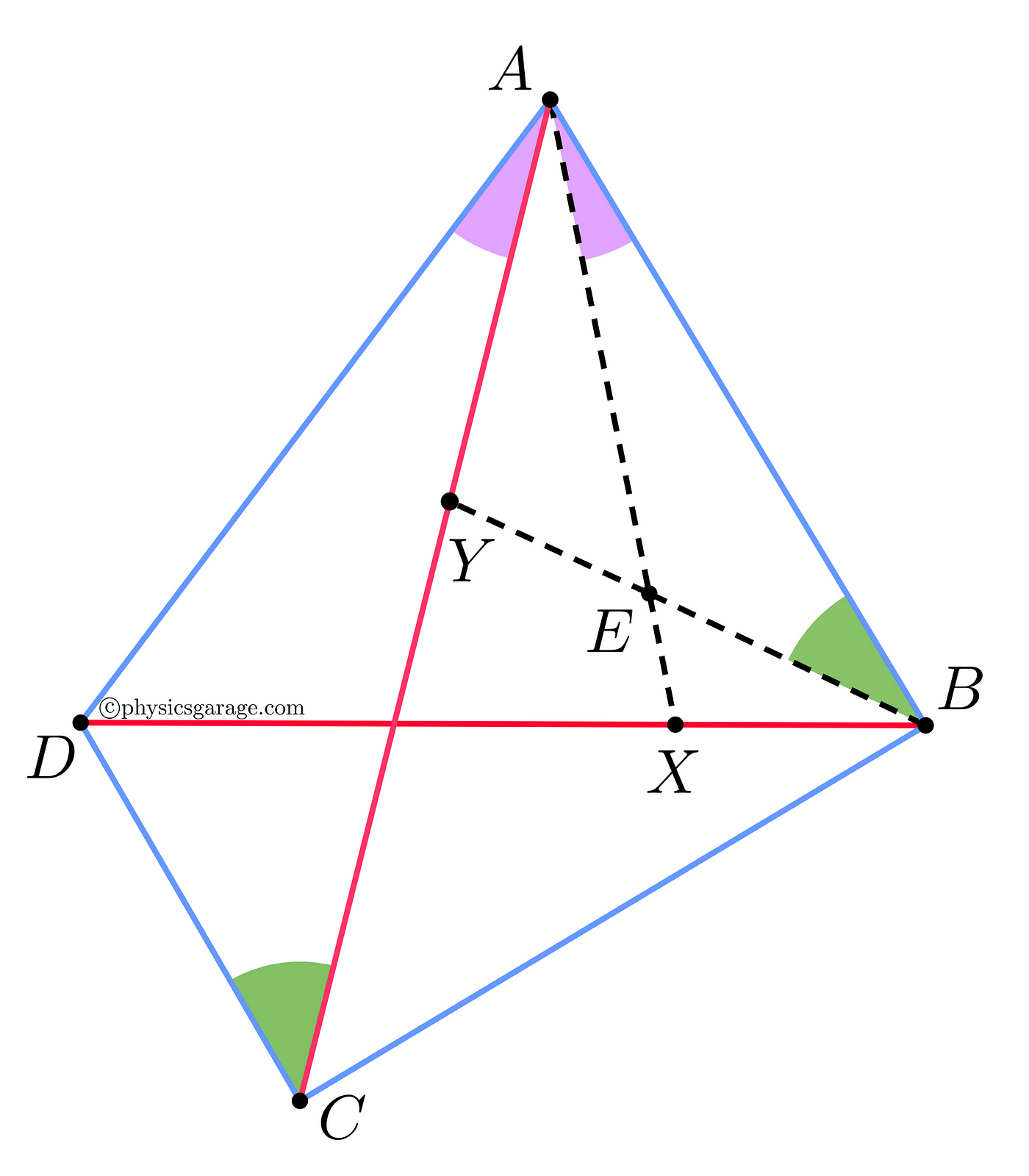
Next, we consider the triangles ΔABE and ΔACD (diagram below),

and observe that -

• ∠ ABE = ∠ ACD (By construction)
• ∠ EAB = ∠ DAC (By construction)

We know that if two corresponding angles of two triangles are equal, then such triangles are called similar triangles. If two triangles are similar then the ratios of the corresponding sides are also equal . That means,

We could also use another pair of sides -

Similarly, we consider another pair of triangles, ΔDAE and ΔCAB (diagram below).

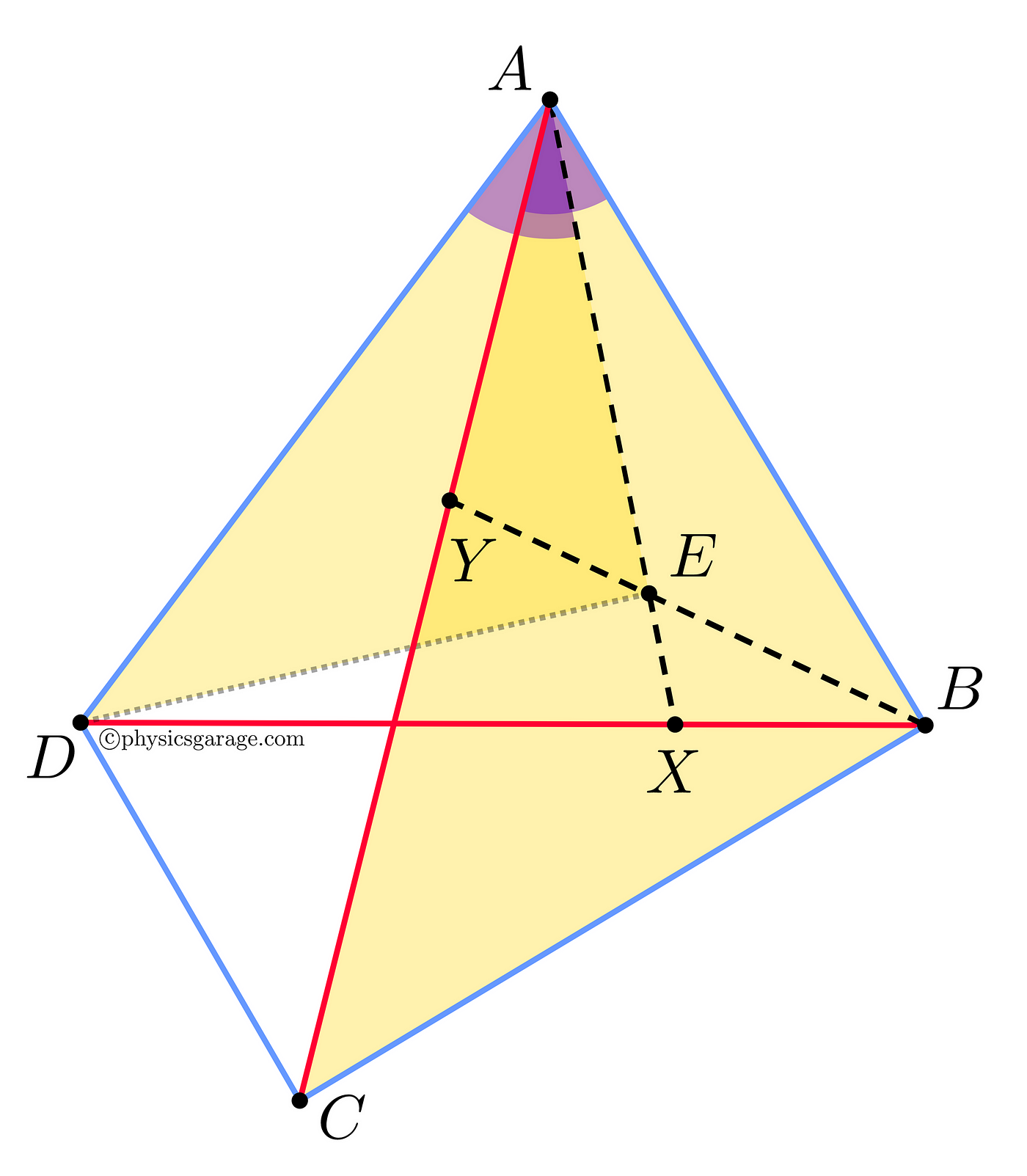
We already know that ∠ DAC = ∠ BAE, by construction. If we add an angle to both sides of the equation, it won’t change anything . So, we add ∠CAE on both sides to get -

But, we can see from the diagram that,

• ∠ DAC + ∠ CAE = ∠ DAE
• ∠ BAE + ∠ CAE = ∠ CAB

Therefore, we can rewrite equation (3) as

Now, looking at equations (2) and (4), we can see that we have satisfied the requirements of similar triangles — this time we have established the equality of one angle and ratio of a pair of sides containing this angle. This is called a Side — Angle — Side criterion of similarity.

If these triangles (ΔDAE and ΔCAB) are similar, we can obtain the equality,

Finally, we add equations (1) and (5), to get

In the beginning of the section, we talked about the existence of a triangle inequality. Now is the time to use it

It states that -

Using this fact, for ΔDEB in the diagram above, we can write -

Therefore, using equation (7) we can write equation (6) as

which is what we wanted to prove.

Inequalities like these are incredibly efficient at solving some really hard problems in mathematics and physics. Next time, we are going to solve a very interesting real world problem, and see exactly why this theorem is incredible!

Originally published at https://physicsgarage.com on April 12, 2020.