Physics Puzzles: Why Satellites Don’t Fall From the Sky

Gravitation is ubiquitous. Its presence is felt at any place. Isolation doesn’t exist in the universe; everything is connected to everything else. A thrown-up apple attracts our planet whereas our planet attracts the apple. Doesn’t it sound great? How cool is that? Whatever you hold in your hand has enough power for moving the Earth. Of course, this effect isn’t any huge but its existence is. I don’t know how about you, but this makes me feel so powerful. Even more, there is a saying that some people are drawn to each other for which, as you now know, a scientific background exists. 😺

What about satellites? Why they don’t fall off when they’re clearly pulling down by the Earth? What keeps them in their orbits? At first glance, it looks like some kind of a magic trick. So, give it a thought. And, maybe you will be able to undress a magician. Just try.

Alright, so all to be noted are the linear velocity and the gravitational force. Plus, for the sake of arguments, a perfectly circular orbit, which, in reality, might and have an elliptical shape.

What is the solution?

Well. Matter of fact, the satellite falls off — just not straight onto the ground. Because by applying the right momentum, it will continue to go around in a circular path.

What does it mean?

Let’s assume for a moment that an object was lifted and left at rest in outer space, what will happen?

Our observer sees the box as going down along a straight line. And, it isn’t any surprise. It’s perfectly logical and in line with our intuition.

A bonus question that I want to address: How this straight-line motion as seen by our observer appears to someone on Earth? Will it be of the same kind, or not? Maybe curved, somehow? (hint, Coriolis force.)

Back on the right track, time to be more qualitative.

The universe doesn’t tick-tock to the universal clock. Passage of time depends on who and from where is looking at. Among observers, the time rate differs by relativistic effects. With approaching the speed of light, it slows down. And, I’m not a fan of this rate of change part. It messes up. Laws of nature need invariants to hold on. Instead of counting seconds, I prefer to think about how many of the primary operations it took. The universe is constantly changing, particles are exchanging their momenta among themselves — we are living in a big boiling soup. By “primary operation”, I mean the discrete behavior of the universe. A single interaction between particles during which their momenta exchange by a tiniest little. Beyond our today’s understanding is how it happens but somehow it does. And, whatever it is, must be a principal of the universe.

Why do I write this down?

Because I want to refer to an abstraction of an infinitely short time, dt. But, instead of thinking about a fraction of a second, I want you to visualize a single primary operation that I wrote about.

During then, gravity pulls the satellite down about a distance, dy. While the aim is to keep it at a constant distance from the Earth. Thus, to make it follows around in a circular path. No other figure than a circle exists that could allow for that. So, to make it happen, a velocity must be applied. But, velocity brings to the table a new set of questions: about the magnitude, and about the direction.

Which direction the velocity has to be directed in?

Well, we might go through geometrical either analytical proof… or make use of our brains. If the direction would be any different than perpendicular to the gravity, it would bring the satellite even closer or advance it even further from the circular orbit. So, the only logical solution is the perpendicular direction.

How to estimate the needed speed, |dx/dt|?

For that, notice that gravity plays the role of a centripetal force,

By matching together with gravity, one could determine the desired magnitude of the velocity. Doing that,

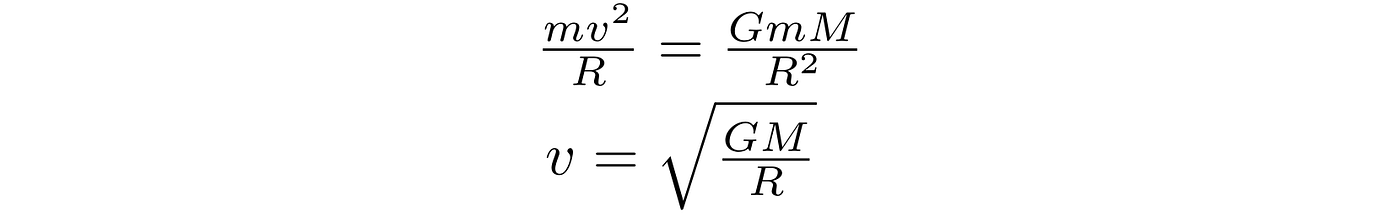
And, that is how it’s done.