I have a habit of throwing into the air whatever I hold. I do it so often that some call it as my addiction, yeah, it is so common to me. Depending on initial conditions, on how it left my hand, I make bare predictions: how many rotations it will make, what hight it will reach, and so on.

Often, when I go across a city, it is just a bottle of water or any other drink (of course, closen: I do not want to become wet 😄,) what makes it even funnier because a decrease in the water’s level changes the behavior of the bottle, by just say — drastically.

On the other hand, when I walk along a river, where many pebbles lay down, I pick the most rounded one for a ride to the air and back. And, here comes the puzzle.

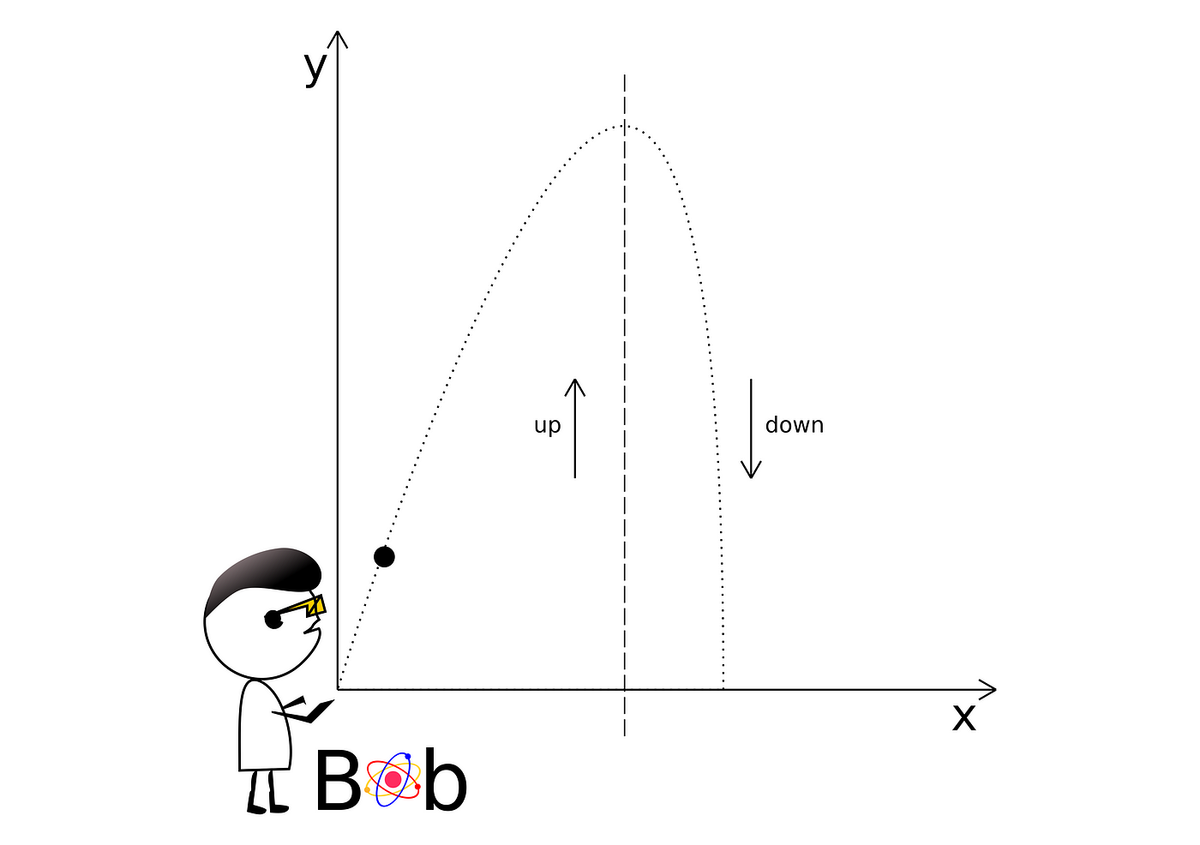
Bob has thrown a pebble into the air from an ideally horizontal ground. It means that it will cover exactly the same vertical length during its up and down motions. Will it take longer for the pebble to rise or fall? (Also, say hello to Bob because he will return every now and then with new puzzles. ✋)

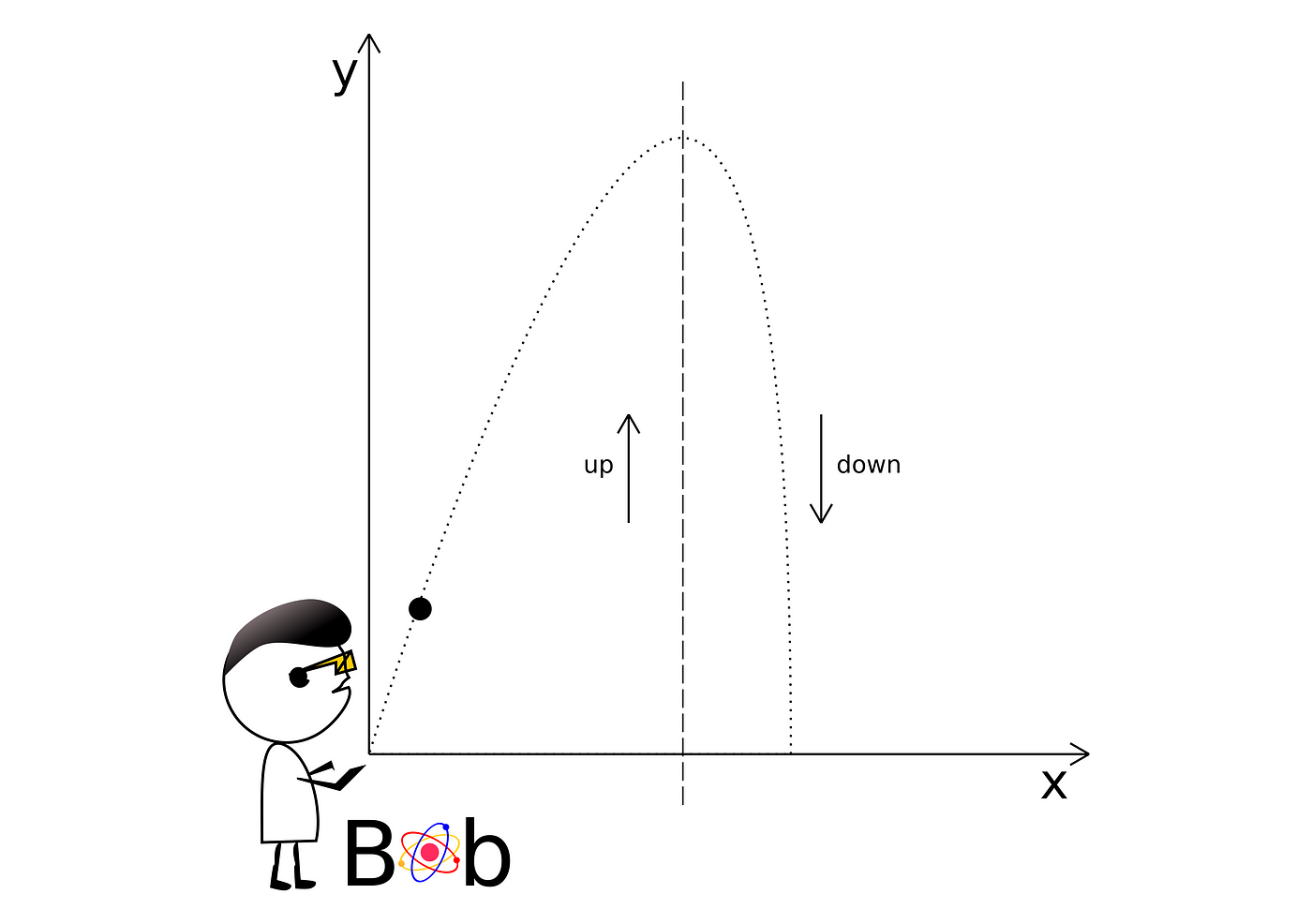
The solution

The velocity of an object is a vector that contains information about its speed and direction of motion.

Galileo’s principle of inertia, Newton’s first law of motion, and the common sense, state that an object at rest, or with constant velocity will keep its state (being at rest, or going in a straight line) in absence of a net-force.

Every time you are about to describe the behavior of an object, you should start by answering if there is a net-force.

How?

Just do an experiment once and the answer pops out immediately.

• If the object’s velocity changes, there is a net-force.
• If it goes in a straight line, without changes its velocity, there is no
  net-force. And the object will maintain its motion forever and ever until some force will not break it from its state.

So, back to the puzzle.

In the absence of a net-force, the pebble would continue its motion in a straight line, like that:

Yet, Bob’s chin would crash with the ground (mine too) if that happens! Because he knows that it cannot be the case!

Every object exerts the gravitational acceleration that depends on its mass and the position of a body on which it acts. For Earth’s nearby bodies, it is well-known, g=9.81m/s². And this value stays constant for any mass. For dust, pebble, you, and me, as long as the distance to the center of our planet stays relatively close, it is always just g. That is the geometrical property of the fabric of space. Many tried to show its dependencies of mass, and they all failed. Some scientists still give it some thoughts, but, most likely, the results of their works are meant to fail.

On a planet, without the atmosphere, the object’s motion would depend only on the gravitational pull and thus take a parabola arc. Because a quadratic function describes the position within the gravitational field; it would imply equal time for going up and down.

But. Here, on Earth, we have the atmosphere, which additionally exerts an air drag on our pebble thus makes the inequality of these times.

Drag force always opposes the object’s velocity. If it tends to go up, the force will act on it towards the down. The faster the object goes, the more molecules it bounces off, which means the drag is proportional to the velocity.

While the pebble goes up, the gravity and drag reinforce since they act in the same direction, towards the down. But, during the fall, the velocity flipped the direction, which makes the drag force flipped also. Hence, the forces oppose each other now.

So, during the fall, the net-force is smaller, which means the acceleration is smaller, which means the pebble will need more time to cover the same distance as during the rise.

The bonus

Do you know why parachutists cannot accelerate beyond a certain speed?

Because after reaching a certain velocity, the drag force opposes in direction and matches in magnitude the gravitational force, which means the net-force acting on a parachutist is 0; he cannot accelerate anymore; the forces “kill” each other, so to speak.

Until next time!