Ramanujan
The Hardy-Ramanujan Number
The two different ways 1729 is expressible as the sum of two cubes are 1³ + 12³ and 9³ + 10³. The number has since become known as the Hardy-Ramanujan number, the second so-called “taxicab number”
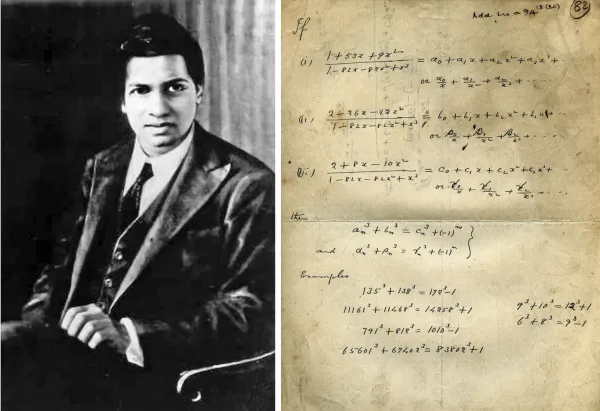
Ramanujan
The two different ways 1729 is expressible as the sum of two cubes are 1³ + 12³ and 9³ + 10³. The number has since become known as the Hardy-Ramanujan number, the second so-called “taxicab number”

Mathematics
Understanding Pierre de Fermat’s observation about prime numbers

Erdős
Paul Erdos is to this day remembered as the man who devoted his entire life to mathematics. Living out of a suitcase traveling from university to university, throughout his life he survived off speaking fees and modest endowments from various universities.
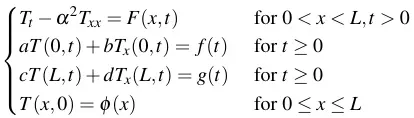
Physics
This is the third article in my series on partial differential equations. Before reading further you might want to read part one (9…
Mathematics
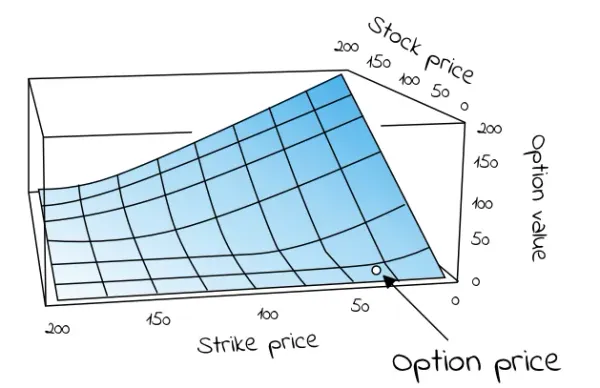
Introduction to the most famous equation in finance
Mathematics
“As Leibniz suggested, we appear to live in the best of all possible worlds, where the computable functions make life predictable enough to be survivable ...
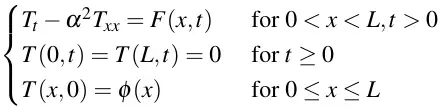
Physics
The inhomogeneous heat equation
Mathematics
The shape of the universe as it was, is now and may become in the future is very hard for us to discern empirically. Einstein helped us somewhat by showing us that matter and energy (three-dimensional phenomena) in fact may interact with the a four-dimensional phenomenon: time
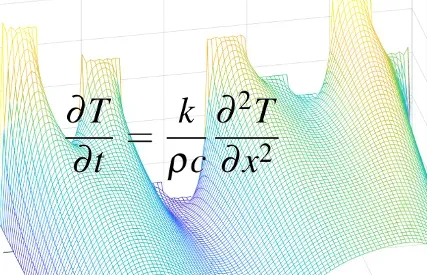
Physics
Your first PDE. Bonus: Fourier series.
Quantum Computing
These days all your devices are encrypted. Your texts, emails, all have …
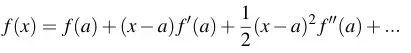
Mathematics
Approximating functions near points. It’s cooler than it sounds, trust me.

Einstein
The published version of a talk by mathematician David Hilbert (1862-1943), dated the 20th of November 1915 is entitled ‘Die Grundlagen der Physik’ (“On the Foundations of Physics”).