Our setting is the open unit disk, D and T the unit circle, in the complex plane, C. By H² is meant the standard Hardy space, the Hilbert space of holomorphic functions in D having square-summable Taylor coefficients at the origin. As usual, H² will be identified with its space of boundary functions, the subspace of L² (of normalized Lebesgue measure m on T) consisting of the functions whose Fourier coefficients with negative indices vanish.

A Toeplitz operator is the compression to H² of a multiplication operator on L². The operators of the paper’s title are compressions of multiplication operators to proper invariant subspaces of the backward shift operator on H². An effort has been exerted to make the paper reasonably self-contained.

Some preparation is needed prior to precise definitions.

We let P denote the
orthogonal projection on L²with range H². The operator P is given explicitly as a Cauchy integral:

We shall need to deal with certain unbounded Toeplitz operators.
The operator T_ϕ, the Toeplitz operator on H² with symbol ϕ, is defined by

We let S denote the unilateral shift operator on H². Its adjoint, the backward
shift, is given by

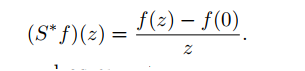
Clearly, a truncated Toeplitz operator does not have a unique symbol.

The compression of S to K_u will be denoted by S_u. Its adjoint, S*_u, is the
restriction of S* to K_u. The operators S_u and S*_u are the truncated Toeplitz operators with symbols z and z, respectively.

The next section contains most of the needed background on the spaces.

Background Materials;

The bulk of it can be found in standard sources;

The model space, as is well known, carries a natural conjugation, an antiunitary involution C, defined by

It preserves the model spaces.

An operator A on model space K_u is called C-symmetric if CAC = A*. S. R. Garcia and M. Putinar study the notion of C-symmetry in the abstract sense. They give many examples, including our truncated Toeplitz operators (at least those with bounded symbols). The following result is essentially theirs.

Let T(K_u) denote the space of all bounded truncated Toeplitz operators defined on the model space K_u.

We have the following results which are called defect operators or rank one operators in terms of reproducing kernel Hilbert spaces.

Condition for A_phi=0;

In this section will characterize the zero truncated Toeplitz operators whose related with its symbol.

The symbol of the truncated Toeplitz operator is not unique. The following corollary shows this…

Characterizations of Truncated Toeplitz Operators;

The bulk of the proof will be accomplished in two lemmas.

The following result is that the space of truncated Toeplitz opertaors is closed in the weak operator topology.

Characterization by Shift Invariance;

Given a bounded operator A on model space K_u, we let Q_A denote the associated quadratic form on K_u,

We shall say that A is shift invariant if

whenever f and Sf are in K_u.

If this happens then, by the polarization identity, we also have

whenever f,g, Sf,Sg are belong to the model space K_u.

Truncated Toeplitz operators can be characterize by using the following theorem.

Crofoot’s Transforms

The following theorem shows that J_w is an isometry between model spaces.

The adjoint of the Crofoot transform is given by

The Crofoot transform of a truncated Toeplitz operator is a
truncated Toeplitz operator on another model space.

The following lemmas can be used to prove the above theorem.