A couple of things before we start, I’m not writing this as an attack, these are just personal view based on some facts. I’ll be using a little bit of math in the part of Game Theory nothing too crazy, I think if you have studied class 12th math you’ll understand it. And finally, please ignore the typos(yes I did use Grammarly).

What is Relative Grading?

The concept of Relative Grading is quite an old one, not sure when it was actually introduced but the papers referencing it go back to the 1970s here. There are quite some reasons why it exists, one of them you might have thought of is the growth of the student population, which correlates to either having bigger classes or having multiple sections for the same course, which would require more teachers, and teachers have different metrics and strategies for grading an answer, which leads to unfairness between the different sections of the same course, relative grading will normalize the variations and put everyone at plain-level field. Another reason is the incentives and the competition, I will go into some depth with this word “incentive ” but to explain it in simple terms, relative grading induces a competition, in the sense that to get a good grade, you’d need a “good” overall score and be better than rest of the class.

Let’s look at an example, now these data points do not represent a real scenario, but they capture what the distribution of marks would look like. Now if you know a bit of statistics, this looks like normal distribution and it is, the most common type there is. If you need a refresher on distributions this is a really good resource.

Now the reason why I personally used a normal distribution is that they sum up the situation really well, right? You have some people who score really well and some who score really bad and the rest are kind of in the middle.

The running assumption in this article is that the tests are fair, which means that there are no errors in the questions and the teacher grades the papers without any bias.

Let’s say, we were to give a grade based just based on this performance. And I will be using the Relative Grading System. The formula for calculating a relative grade is quite straight forward, it only differs in what grading system you are using.

Now let’s see how our program based students performed.

I’d say pretty good right, the majority got A and B, and then we have the 20 or so super nerds who got the S, remember this is out of 500, so if you assume the class size to be 60, the people who got an S will be in the range of 3–6 and so will be the F’s. Now, this does prove that in order to get the best grade you have to be better than the rest but the data in practice isn’t as beautifully distributed, it would probably be a skew-normal distribution which would look like this because believe it or not scoring below 10 on a 30 mark exam whose average is 23, is pretty hard.

And here are the grades.

So it is quite apparent that as the mean increases the number of S grades decreases and the distribution becomes more centered to B. And it's this result which directs the sentiment behind this article.

Game Theory And Exams

Game Theory, if you are a movie fanatic, you might have watched Russel Crowe’s “A Beautiful Mind”, which good film but modern cinema has this thing that a story has to be dramatic to be good, so for the people who haven't watched it now you know what to expect. A little about the field itself: It started with Plato when he described the Battle Of Delium in his piece Laches, the first mathematical formulation was done by John von Neuman, where non-mathematically speaking we can always find an equilibrium in a finite two-player game(I will define all these buzzwords, don’t worry) and John Nash who proved that equilibrium exists even in an n-player game. In this section, I wouldn’t dive very deep into mathematics(some), we’ll keep it philosophical and the field of Game Theory is extensive, there is no end, mathematically and definitely not philosophically, so I encourage you to read more about it, and appreciate it’s beauty in mathematically addressing human psychology.

What is a Game?

A game in a very “non-gamer” sense is a situation whose results depend on the actions of the parties involved.

Let’s break it down. The parties involved are called players, these are the entities that take actions that affect the state of the game. Now, why are players even interested in taking an action, well they’ll get a reward if they take an action that benefits himself/herself. This reward is defined by a utility function or payoff function, which is just a mapping of the actions of a player to a real number. So a finite n-person game is a tuple with (N, A,u) where N is the number of players, Ais the action set(the set of all actions that will be taken by any player, you can also call it action space) and u which is the utility function. So let’s formulate them mathematically

Now that we have a naive understanding let’s look at the things that actually matter. We know that a player gets a reward for playing a good strategy, so the goal is to maximize the utility function by using the actions available in the action space, now if I know or have some intuition on what the other players will do, I can tailor my actions in order to get the highest utility, this is known as Best Response, which basically is the means that the reward I will get by playing the best response action is will be greater than any other possible set of actions. So, to understand this in a more mathematical sense,

I hope you are still with me, it’s all philosophy from now on I promise.

If every player plays his/her best response, we achieve a Nash Equilibria. Ok, if you paid attention till now you can probably imagine how Nash equilibria can be used to define human behavior in competitive environments. Although Nash Equilibrium has lead to tremendous success in economics specifically in competitive markets and auctions, it is not limited to that we can see the use of game theory even in biology and education which we will discuss in the next subsection.

Exams

As we saw game theory can be used in a competitive environment, so let’s start and break down exams, into the components we saw in the previous section.

1. Players: You are a player, I'm a player and other students in the class are players
2. Reward: Marks, Marks, Marks***
3. Action: Marking an answer.

Now this feels very ambiguous right? Marking answers will help me score well but how me marking an answer is affecting the other student, and where does the concept of best response fit into this. Well, first-off this will only be valid for a relative system(I will explain the absolute system as well) so if the majority of the players mark A as the answer but the correct answer is B and you mark B then this is your best response, but in this case, you don’t know what the other players are doing and thinking, so you have to play for yourself without the knowledge of the strategies of other players, and there is a term for this but if you think hard about it, you can assign a positive probability to the possible set of answers, this is also called Pure Strategy. So now that we have formalized exams that are relatively graded are games let’s see how rewards and incentives work.

In an absolute graded system, the players are independent and the actions of one player don’t affect the state of the game or any other players.

Now the goal of every player is to perform its best to reach the Nash Equilibria, in an exam if everyone performs for the maximum utility the mean of the class would by 30 and the standard deviation would be 0 and the whole class will get an F.

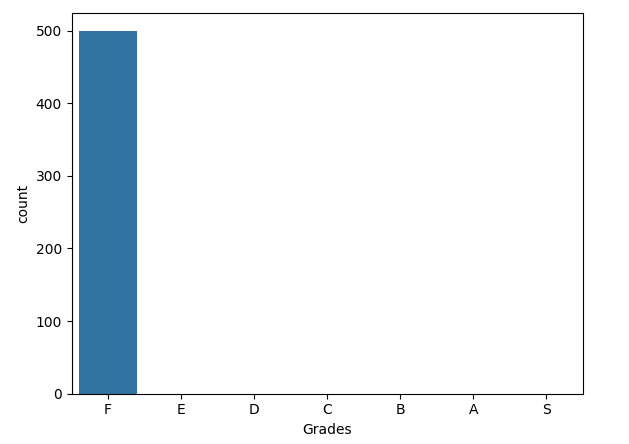
And just in case you are wondering it is impossible that a whole class gets an S, I encourage you to work it out. So one inference you can make the incentive to perform isn't marks, its grades.

Cheater Cheater!!

Again I’m not writing this because I’m pissed about people cheating like crazy in a 30 marks MCQ test, I just want to enlighten them about the repercussions of their actions.

So let’s say you got the question paper and you start solving it and you are pretty confident about your capabilities so you know the answers you marked are correct. In the last 20min of the quiz you open telegram or WhatsApp where people have shared their answers, now you know exactly what other players are doing, and your task is the give the best response which is the correct answer. By now, one of thee things is happening:

1. Your answers exactly match with the answers of other players
2. Your answers somewhat match the answers of the other players
3. Your answers are totally different from the answers of other players

If you are in the first situation, you wouldn't change your answers because of the Bandwagon effect. In the rest, you might. So in order to give what you saw was the best response you change your answers. Again two things happen,

1. The answers were right and you get 30 on 30
2. The answers were wrong and you lost marks

If you analyze the first situation it is pretty bad as well, almost like the fruit of a poisonous tree. And you know why because the mean would shift very close to 30 and the standard deviation would be low as well and hence you will get a graph like this,

And the curve for the grades will look like this,

Looks seeming normal right, except it’s not. To get an S you absolutely have to get a 30 and to get an A, your score should be between 28.5 and 29.5 but its MCQ right so you gotta round that, so having a score between 29 and 30 will get you an A.

If it is the other way round, you marked the wrong answers and even the other players did, the damage wouldn't be as significant But if you marked the wrong answers and other players didn’t such that the difference between you and the average is of 5 marks, you’ll either get a C or a D.

Think about this for a second.

If you are aware, and you know if you cheat this could happen you’d never cheat right? But as humans, (it’s about to get 100% philosophical now) we would be in a situation where we score more regardless of the performance of others, and here lies that incentive to cheat. To make up for the uncertainty we believe anything presented to us. Also if you don't cheat and everyone else is cheating, after some time even you might succumb to it. This is what the modern education system has done, there is so much focus on marks that we have taken a tangent from actually being open to learning to cramming on a constrained syllabus. But let’s say nobody cheats, the curve would look like Figure 2, and we wouldn't have the crazy numbers as we saw in the last paragraph and the grading would actually be fair.

Conclusion

1. After discussing game theory and statistics I hope you now know what drastic impact would cheating on a test create.
2. The education system today is very “marks-centric” that is you can’t get that far if your scores aren’t on point and of course, there are exceptions. But this has created this longing of marks rather than knowledge.
3. Cheating on a test, that is relatively graded has disastrous implications, and it's better not to do it.

References

All the references are added as links. The code will be provided on request.