In this article, I will describe two simple proofs of the irrationality of the Euler number (or Napier’s constant) e ≈2.71828. The first proof is by the French mathematician and physicist Joseph Fourier. The second proof is by the French mathematician Charles Hermite, with details latter published by the Canadian-American mathematician Ivan M. Niven.

A Brief History of e

The discovery of the constant e is credited to Jacob Bernoulli, one of the many renowned mathematicians in the Bernoulli family, when he was attempting to find the limit

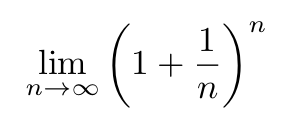
which is equal to e. The constant, represented originally by the letter b, was first used in letters exchanged between the German polymath Gottfried Leibniz and the Dutch physicist and mathematician Christiaan Huygens in 1690 and 1691. However, it was the mathematician Leonhard Euler who introduced the symbol ein a letter to the German mathematician Christian Goldbach in 1731. The first occurrence of e in a publication was in Euler’s 1736 book Mechanica.

The constant e can also be obtained via an infinite series:

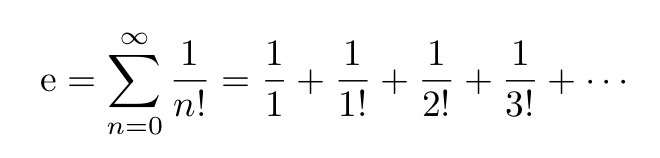
Irrational numbers

Irrational numbers are real numbers that cannot be constructed from ratios of integers. Among the set of irrational numbers, two famous constants are e and π. In one of my previous articles (see link below), the irrationality of π was proved. In the present one, I will describe two proofs of the irrationally of e.

In the figure below, the real number set diagram is shown. The transcendental numbers are numbers that are not roots of polynomials with rational coefficients. Some irrational numbers are transcendental (such as e and π), but some are not. The latter are called algebraic numbers and can be roots of non-zero polynomials with rational coefficients.

Proving the Irrationality of πA Simple Proof of a Remarkable Resulttowardsdatascience.com

Proofs By Contradictions

A proof by contradiction is a type of proof that determines the truth of a proposition by showing that if one assumes the proposition to be false, one is led to a contradiction. It is a particular case of the argument known as reductio ad absurdum.

“Reductio ad absurdum, which Euclid loved so much, is one of a mathematician’s finest weapons. It is a far finer gambit than any chess play: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.”

— G.H. Hardy

As mentioned in the introduction, the goal of this article is to prove that e is irrational. Two proofs will be given, both proofs by contradiction. They are:

• Proof I: A proof that e is irrational that is based on the use of infinite series and was devised by Joseph Fourier.
• Proof II: A proof that eʳ is irrational, where r is any nonzero rational number. This proof was devised by Charles Hermite and Ivan M. Niven and it is more general than Proof I.

The Proofs

Let us start with the simpler but less general first proof (see Simmons).

Proof I: e is irrational.

We can rewrite Eq. 2 as follows:

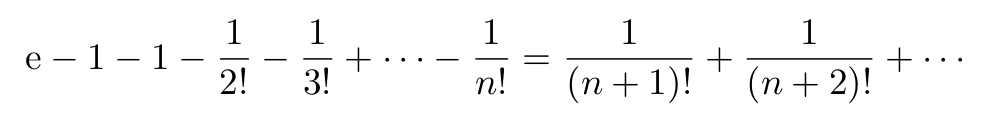
Since the right-hand side of this equality is obviously positive, we conclude that its left-hand side is also a positive number for any positive integer n. Now suppose that e is rational:

Now, for any q we can always choose a value of n such that n>q. Our next step is to define the following number a:

Since n>q, n! is divisible by q:

which implies that the number a in Eq. 5 is a positive integer (recall that we assumed that e is rational). However, using Eq. 3 we find that

which contradicts our previous result that a is a positive integer. We conclude therefore that our initial assumption that e is rational must be false.

One of the first publications of this proof appeared on the 1815 book “Mélanges d’Analyse Algébrique et de Géométrie” (A mixture of Algebraic Analysis and Geometry) by Janot de Stainville. Pages containing part of the proof are shown below in Fig. 4.

Proof II: eʳ is irrational, where r is any nonzero rational number.

Let us now consider the second proof of the irrationality of e (see Simmons)

For this proof we will use the following auxiliary function:

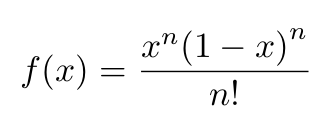
where n is an integer. This function can be written as a power expansion:

For example, for n = 1 and 2 we have:

For 0< x < 1 the following inequalities are obeyed:

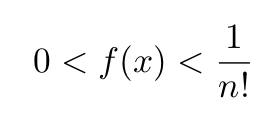
The proof of Eq. 11 can be found in one of my recent articles. Three other properties of f(x) will be needed. Two of them are:

where (m) represents the m-th derivative. The third property is:

which is an integer number. Note that:

• f(x) and all its derivatives are integers at x=0
• Since f(x) remains the same if we interchange x by 1-x (and vice-versa), the function itself and its derivatives are also integers at x=1.

Now let r=p/q and eʳ be rational numbers. We then have:

It is therefore sufficient to prove that eᵖ is irrational for every positive integer p. We now assume that eᵖ=a/b for integers a and b and define the following function F(x):

It is not difficult to verify that F(0) and F(1) are integers. We then integrate the following equality

between 0 and 1. The result is an integer number:

However, using Eq. 11 we obtain:

Comparing the last two equations we arrive at:

According to Eq. 18, the expression between the inequalities cannot be a positive integer. But this contradicts Eq. 17 which implies that eʳ cannot be a rational number. Choosing r=1 we find that e is irrational as well, which concludes our proof.

My Github and personal website www.marcotavora.me have some other interesting material both about mathematics and other topics such as physics, data science, and finance. Check them out!