Understanding the sun-to-planets absolute distances was a long-run investigation proceeding with new scientific-tools and new laws. As a police case requires time and symmetry of action that concatenates all threads within one bracket, space exploration is alike.

At the time of Venus transit in 1761, scientists had all to kill the bird once and for all. Equipped with a plan born in Halley’s mind, they got up to work; and passed, being only 2–3% offs.

However, years before, even excluding the ancient Greece astronomers, attempts were made by many others, among which was one by Jeremy Horrocks in 1639.

This story is to show the Horrocks’ way, whereas the next will be about Halley’s one.

Jeremy Horrocks’ way

In Horrocks’ times, astronomers believed the distribution of planets is not a mere coincidence but bare a relationship to their sizes.

And they had premises to though like that.

Copernicus heliocentric system in which planets revolve around the Sun in perfectly circular orbits (corrected by Keppler to elliptical shapes;) laws on planetary motions and relative planets-Sun distances; observations of inferior and superior conjunctions, especially of Mercury and Venus, all were building up this hypothesis.

On the 7th of November 1631, Pierre Gassendi observed and collected data of the Mercury transit predicted by Keppler on that day. That, along with Horrocks’ own observation of the 8-years-later Venus transit, led Horrocks to presume that all planets viewed from the Sun subtend an angle of 28'’ as for both transits’ calculation, it was the case; more or less. And so, he took it as too unlikely to be an accident. Even though he believed in the result, he had known that this is just a probability. As said,

I do not put forward this conjecture as a certain demonstration but as a probability.

Nevertheless, with such law, he was able to guess the distance of Earth to the Sun. Improperly because it is just wrong, but still.

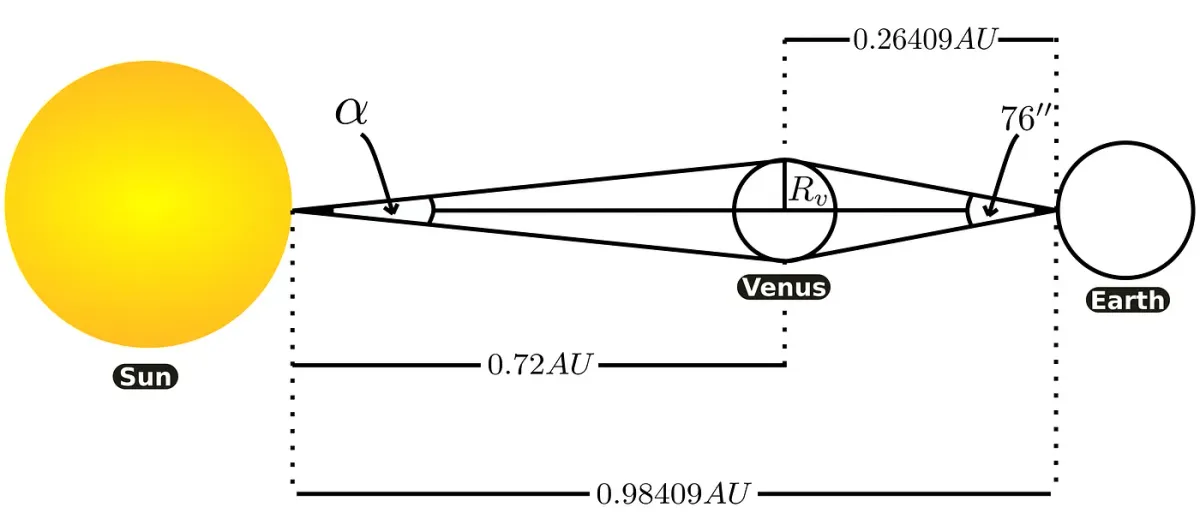
The 28'’ calculation of Venus transit

The 17th-century astronomers were using “Rudolphine tables,” a collection of stars and planets’ positions in the sky, to determine future events. This data successfully predicted the Mercury transit in 1631 but contained no information about the transit of Venus in 1639 as showing it to be a slight-miss. Yet, Horrocks with William Crabtree had shown that the transit is going to take place.

He was prepared and made observations of Venus’ angular diameter to be 76'’. He included a small deviation from Keppler’s distances due to the orbital eccentricities of Earth and Venus at that day and got an angle of 28'’ as Venus would look observable from the Sun.

The configuration was like this:

The tangent value for Earth:

The tangent value for Sun

Putting together both equations for R_{v}:

Calculating α from it,

gives:

which was approximately the same for Mercury transit.

The calculation of the Sun-Earth distance

Assuming that all planets subtend 28'’ angle as viewed from the Sun,

taking the tangent:

rearranging terms (the value used for Earth’s radius was somewhere between 5800 and 6900 km:)

which gives:

Pretty nice estimation; however, incorrect assumptions made it just wrong.

Almost there, now. The next time, following James Short’s calculation based on Horrocks’ idea, the Astronomical Unit will appear close to what it is today.