Electricity, Gravity and Statics

Electromagnetism as compared to gravitoelectromagnetism (GEM) was formulated by the proponents through painstaking observations on the behavior of real objects, i.e. magnets and inductors in their respective electric and magnetic fields. A similar observation on a gravitational field, while it would seemingly be easy, is on the contrary counterintuitive, especially when the supposed objects possesses both particle and wave-like properties of significantly foreign aspects. As a result, researchers have mainly focused on theorizing the similarity between electromagnetism and gravity in order to study the gravitational field¹²³⁴.

Today Electrogravitostatics — a terminology to explain the relationship between all the three aspects, is a gray area even though a lot of research is currently on focus. Instead of heading directly to the complex equations of electromagnetism, in this essay we will first explain gravitational potential energy as a somehow clear case that binds the three components together. We will then attempt to come up with relevant equations relating to electrogravitostatics.

From Gravity to Electricity

We will set up a number of comparative analogs between gravitational, electric, and magnetic fields. Suspended objects possess, rather gains energy purely due to their positions and a change in masses relative to the ground on Earth surface — this is referred to as gravitational potential energy. In practice, this is the form that we convert to electricity, for instance through the generation of hydroelectricity, and is calculated as E = mgH, the product of mass, gravitational strength, and the object’s height, or its position relative to the ground. In hydroelectric power generation, the logic being, water falling from a defined height H (say of a waterfall), is run through the blades of a turbine (Fig. 1), turning it into a mechanical rotating machine. From here, electromagnetics as formulated by James Clark Maxwell takes over. Located at the center of the turbine is a rotating field magnet and a stationary armature (look up this word).

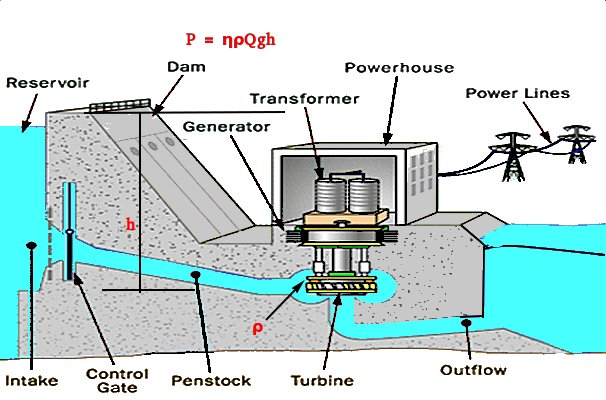
When the mass is expressed as a function of density, m=ρ V, and time derivative dE/dt is taken, assuming a continuous function as of fluid, we get the power, P generated by the object such that P=ρgHQ. In the case of hydroelectricity, Q is the volumetric flow rate of water. An extra term, η is however introduced to correct such obtained power, leading to Euler equation P =ηρgH Q, where η is the turbine’s efficiency.

Gravity and Statics

What we explained in the previous section is nothing new. The actual meat on the bone is how (upon raising) a massive object gains the gravitational potential that would be converted to mechanical and consequently electrical energy — gravitostatics. To understand this, you will want to answer these two questions:

• How high would you have to raise a body of mass m, in order to attain the total energy E=mc² predicted by Albert Einstein?
• What are the trends in gravitational potential energy density as H increases?

The short answer to the first question is, it never happens. The explanation is given by answering the second question. The maximum gravitational energy possible is such that:

Now, the real question is how does this happen?

Assuming the mass remains constant, the only explanation that can be given is that the energy density of a body reduces when moved away from a gravitational field. That is to imply, for every meter you raise a mass m, away from the Earth surface, its internal energy reduces purely due to position. This rate of change is given by:

Where, ∇ is nabla — an operand for spatial derivative (wrt H), ρ is the mass-energy density in joules per kilogram, rₛ is the Schwarzschild radius of the object, and r is its radius, c is the speed of light. Eq. (2) is what gravity really is, when the object under investigation is taken to be Earth. Therefore, the maximum value of H you are looking for (in the first question) is given by:

When Eq. (2–3) are applied to Earth as a planet, we get the properties of Earth’s gravitational field as follows:

Explaining the Change in Potential Energy Density

The scenario in the outgoing sections implies that any object moved away from a gravitational field, e.g. elevated over the Earth surface loses energy, and thus it is no longer E=mc² in the strictest definition. FYI, E=mc² is an abbreviated version, since the full version contains both rest and relativistic masses such that E² = m²c⁴ + p²c². Therefore the shorter version is normally used for stationary bodies since they posses no momentum, i.e. p=0.

We are now alluding that relativistic (p²c²) is not the only component to be eliminated due to rest conditions, there is reduction in mass-energy just by moving the object away from the Earth surface. This energy is equivalent to the gravitational potential E=-mgH, and is static in nature since it is lost back when the object is restored to the ground, and hence what we refer to simply as potential energy. It is as though the body gets charged and discharged when raised or lowered respectively over the surface of Earth.

How this Compares with Electrostatics

You might have noticed above system doesn’t look like the statics you know. One hypothesis is to think this way: there is no difference between pulling a part two stuck magnets, and lifting an object from the ground in that, the forces acting are the same but the fields are different. One is magnetic field, the other is gravitational field. Such bodies elevated over a gravity field gains mass, more like when magnets suck all steel fillings around, and seemingly becoming one large of object.

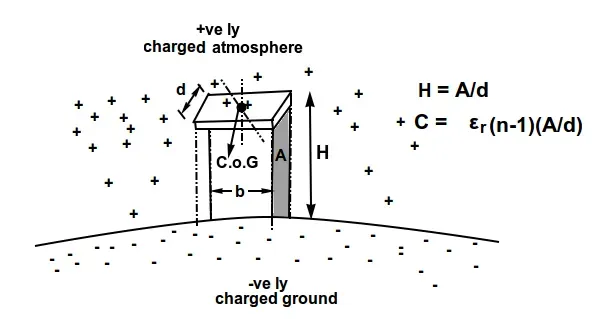
An even better way to see this is by recalling a phenomenon first observed by Dr. William Wall in 1708. He noticed what is now referred to as global atmospheric electrical circuit⁵, in which the atmosphere is positively charged while the ground surface of Earth has a negative charge (see Fig. 2).

Looking at it in that sense therefore allows us to hypothesize that any object elevated from the ground instantly forms a two-plate capacitor with the first “plate” being the surface of Earth, while the second one is the object itself. We also remember from basic electrostatics that for a two plate capacitor, the capacitance C, is estimated by multiplying the relative permittivity εᵣ, with the total number of plates, and the separation distance H = A/d — in Fig. 2. Notice that since n=2, and εᵣ=1 (for vacuum and air), the capacitance thus generated is exactly equal to the height Hin quantity, but with the units of Farads. For such a capacitor, the total stored energy is given by E=CV². We seem to know what the energy is from gravitational potential, E = mgH, the capacitance equation is a shown in the illustration. We can therefore solve for the voltage equivalent of gravitational field energy as follows:

Going by Eq. (5), the voltage equivalent of a free falling body must be given as:

True enough, we can then substitute the capacitance C, and the voltage obtained in Eq. (6) onto the conventional formula E=CV² to obtain the following:

We can also validate Eq. (7) by substituting the maximum height and g obtained in (Eq.3–4) to get the maximum gravitational potential energy Eq. (1) in the following manner:

Past studies equate mass to charge when estimating Lorentz force in Maxwell-like equations. This, in truth is unacceptable for two reasons, gravity is currently assumed to be a mono-pole, meaning it has no North of South pole like ordinary magnets. Secondly, when that comparison is made, there is an overlap between charge units and mass, making it an obvious mistake that raises nonconformity to the fundamental laws of physics and mathematics.

The significance of this method will therefore help anyone trying to relate gravitational field studies to electromagnetism. For instance, following the above methodology, one can expressly write the charge equivalent of mass now as:

Conclusion

As a concluding remark, the above system of equations are fully commensurate with all the laws of physics and mathematics, and are dimensionally sound. It is evident also that they obey other electrostatic methods such as q=CV, not mentioned here, as well as reducing it back to E=CV². More importantly, mass is no longer equated directly to charge, but it’s own charge equivalent must always be estimated through the method presented in Eq. (9).

References

¹ Heaviside, O., 1893. A gravitational and electromagnetic analogy. The Electrician, 31(18), pp.5125–5134.

² Padmanabhan, T., 2010. Thermodynamical aspects of gravity: new insights. Reports on Progress in Physics, 73(4), p.046901.

³ Bakopoulos, A., 2016. Gravitoelectromagnetism: Basic principles, novel approaches and their application to Electromagnetism. arXiv preprint arXiv:1610.08357.

⁴ López, G.V., 2018. On Maxwell Equations for Gravitational Field. Journal of Applied Mathematics and Physics, 6(04), p.932.

⁵ Harrison, R.G., 2011. Fair weather atmospheric electricity. In Journal of Physics: Conference Series (Vol. 301, №1, p. 012001). IOP Publishing.