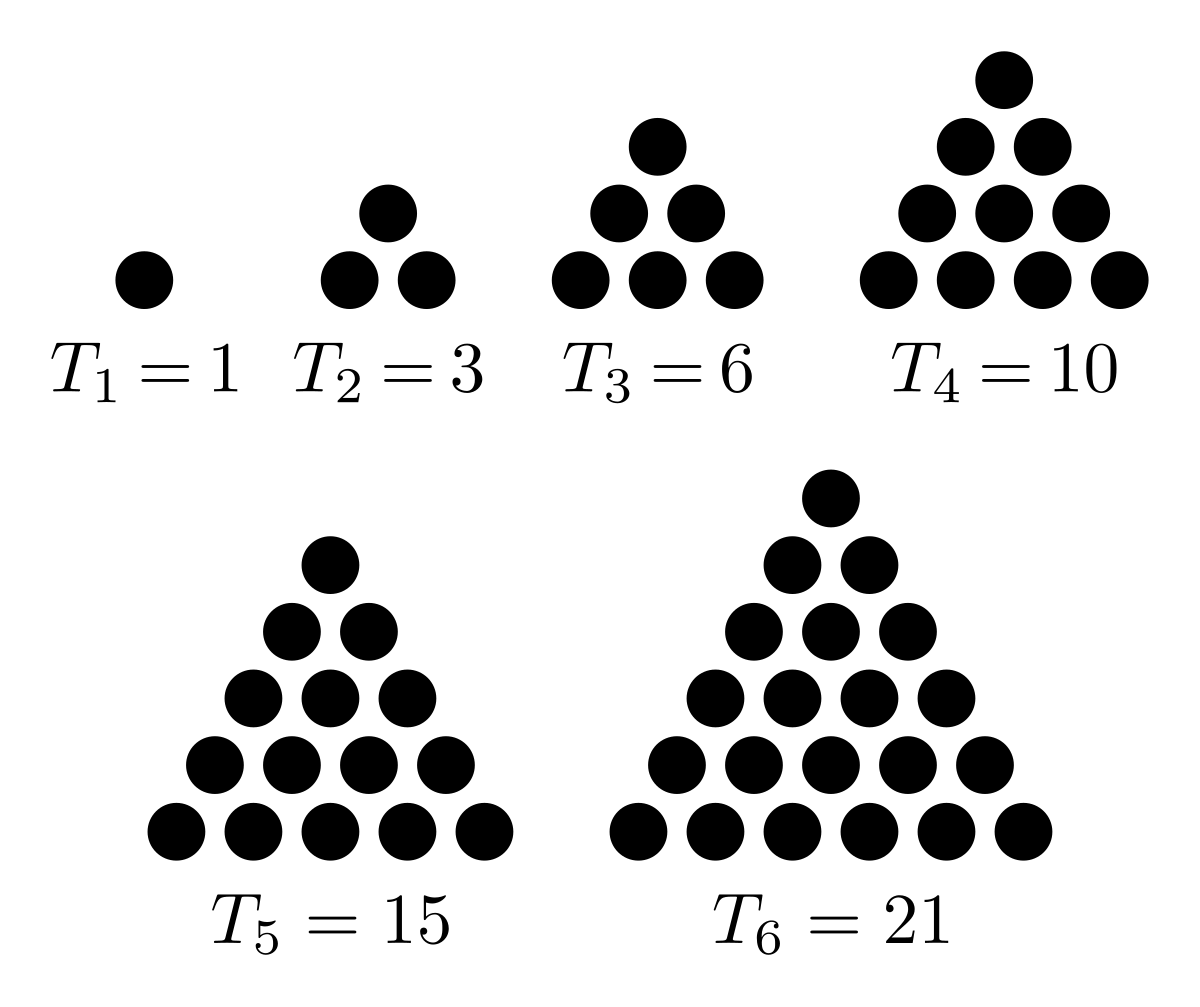Cantor Pairing Function
Represent an ordered pair of integers with a single integer.
Represent an ordered pair of integers with a single integer.
I wanted to create a lookup table for the coordinate points in the first quadrant of a graph. Searching the look up table would be optimal if instead of storing the coordinates as a tuple of (x, y), it could be condensed to a single element.
Thats when I stumbled on the cantor pairing function which would provide a collision free key for each coordinate point in the first quadrant of a graph.
The cantor pairing function is used to uniquely identify a two tuple integer.
The Algorithm
Before we being with the Algorithm, let me explain what is a Triangular Number.
Triangular Number
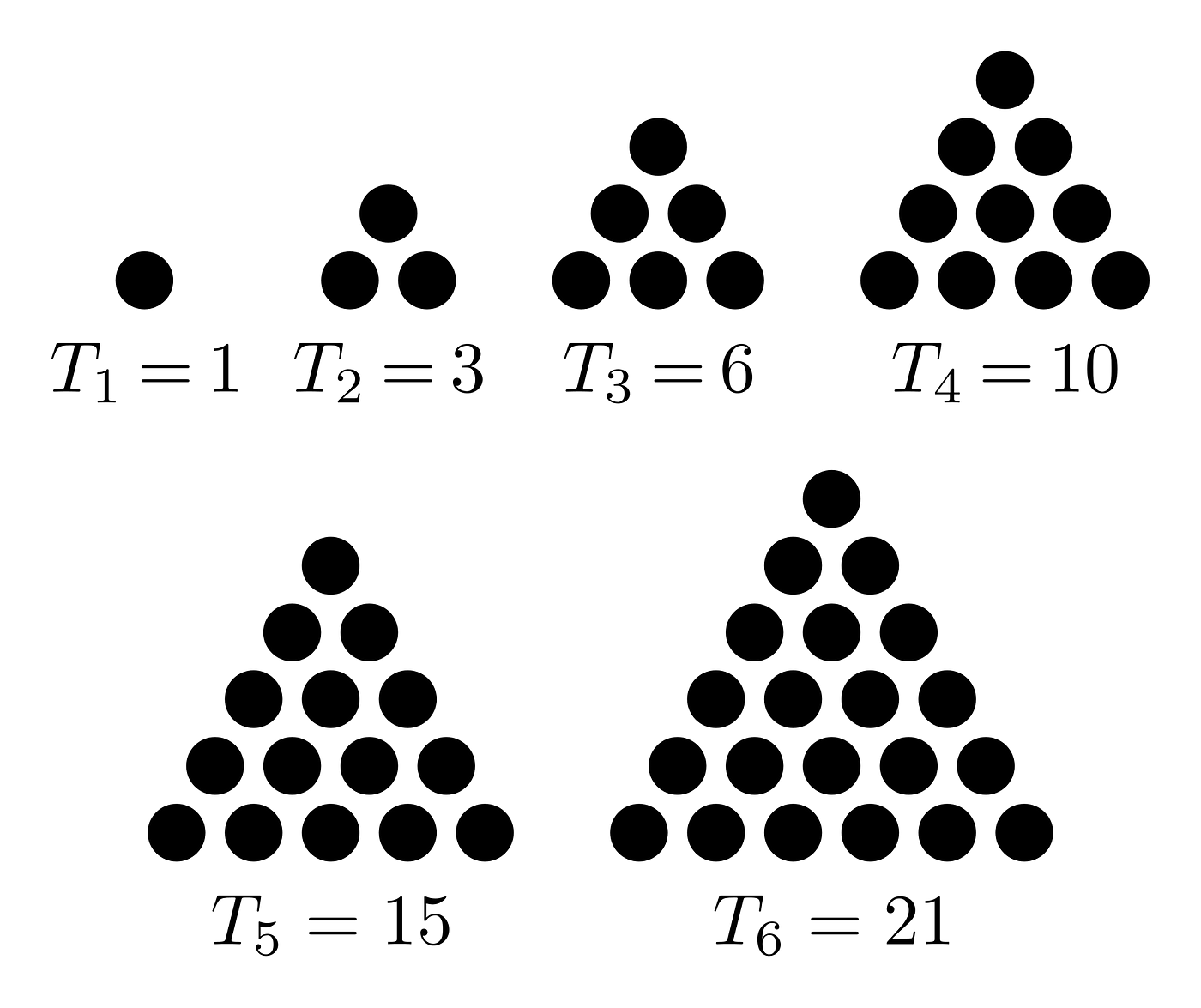
Triangular number is a function that given a number computes the number of dots if it were to form an equilateral triangle as shown above. In short, it is the sum of all the digits up to that number. The formula would be as follows:
triangularNumber(k) = k(k+1)/2;
Computing the Cantor Function
The triangular number function may be used to computer the cantor pairing of two numbers.
int cantorFunction(int k1, int k2) {
int sum = k1 + k2;
int triangularNumberOfSum = triangularNumber(sum);
return (triangularNumberOfSum + k2);
}
The formula for cantor pairing function can also be written as
cantorFunction(k1, k2) = (k1 + k2)(k1 + k2 + 1)/2 + k2;
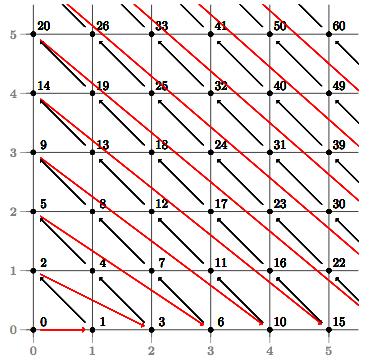
On Graphically plotting the function with k1 on the x-axis and k2 on the y-axis.
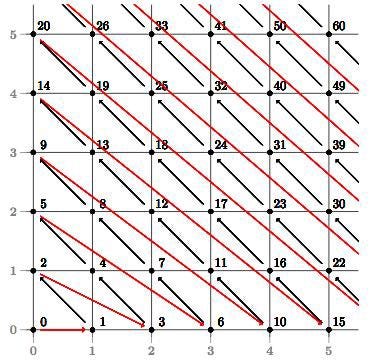
Understanding the function
As shown in the graph, the function increments diagonally upwards towards the left(black line). On reaching the y axis, it restarts from the next integer in the x-axis(red line). Also the pairing function is unique for all values of k1 and k2. It is also noted that the values on the x-axis (0, 1, 3, 6, 10, …) are the triangular numbers.
With this, a two tuple integer may be stored as a single integer.
Also note:
// for all a != b
int u = cantorPairing(a, b);
int v = cantorPairing(b, a);
u == v // returns false
Matrix
The below matrix represents the values of the pair adjacent to the pair (k1, k2). If the Cantor pairing function outputs the value ‘t’ for (k1, k2), the values of the adjacent pairs would be as follows:
262588213843476
References and materials from:
Contributors to Wikimedia projects
262588213843476
