One can occasionally feel sorry for the Flat Earthers. It is quite possible to live an entire human life without encountering any first-hand evidence of the curvature of the Earth. As such, it is easy to see why some might believe such an outlandish theory in a society where we are increasingly being told to trust our own minds and senses above the espousals of the experts.

And yet, we know the Earth is not flat. So why, in our day-to-day existence, does it appear like it is? It’s an issue of scale: we are puny enough relative to the planet that it curves too slowly to be noticed over typical human distances. Only if we move further away from the surface, such as in an aeroplane, can we observe the true nature of our planet directly.

Mathematically, we would describe the Earth as what is known as a manifold. A manifold is any shape or object which, when observed at a close enough distance, behaves as if it were “flat”. When we zoom into a manifold, any region of the object obeys Euclidian geometry. This is the geometry we all learn in primary school: the angles of a triangle add up to 180 degrees, parallel lines stay the same distance apart, and so on.

This is why, if we ignore such complications as mountains and valleys which are insignificant on the scale of the Earth, we see the world around us as flat. The Earth is essentially spherical (sorry flat earthers), and, as humans, we spend most of our lives close enough to its surface that its manifold nature comes to the fore.

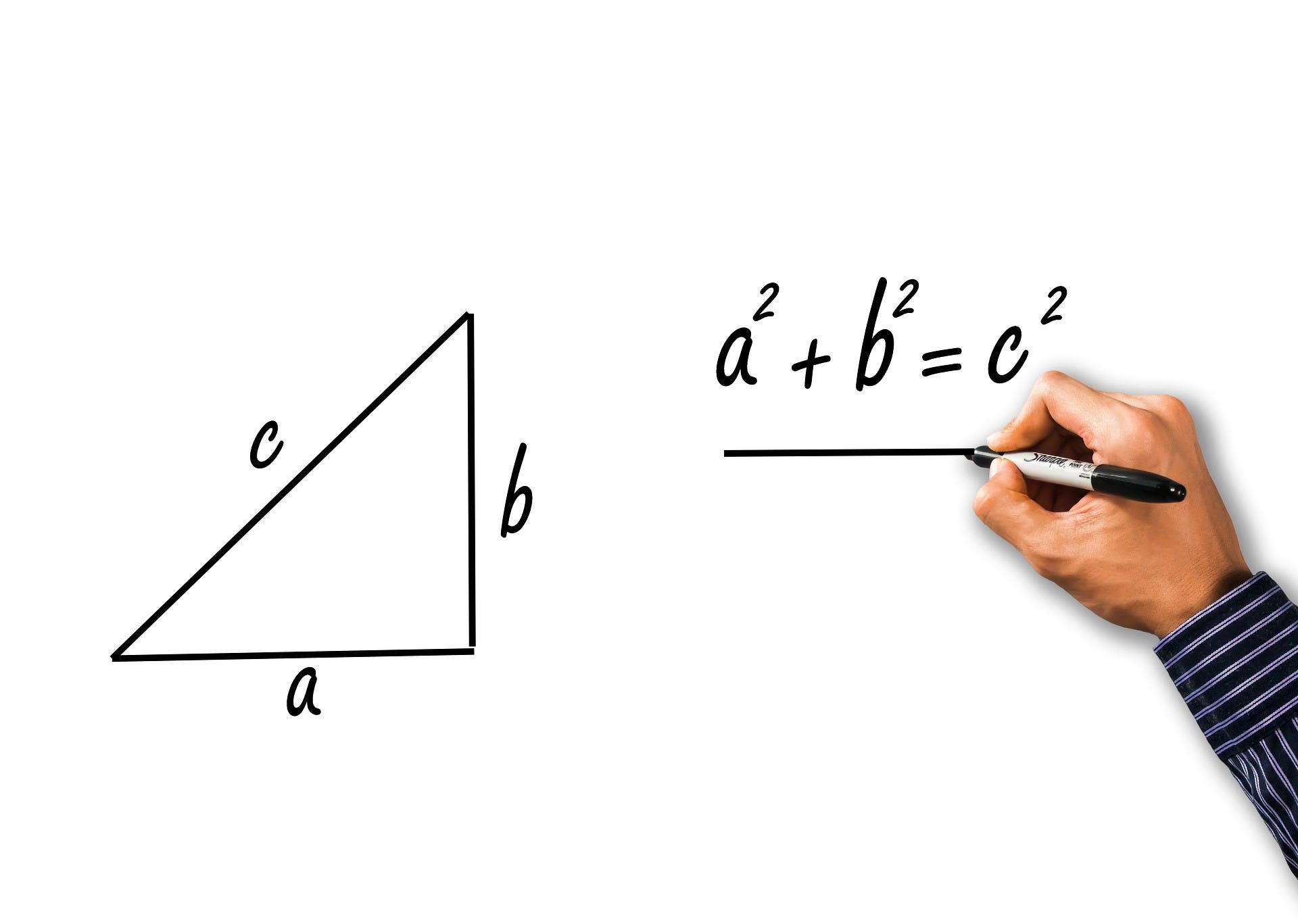
For example, imagine I was standing on a football field by one of the corner flags. Any high schooler could tell me that the shortest distance between me and the corner flag diagonally opposite is a straight line between the two points, as would be predicted by Euclidean geometry. On the scale of a football pitch, the Earth is a flat, Euclidean surface.

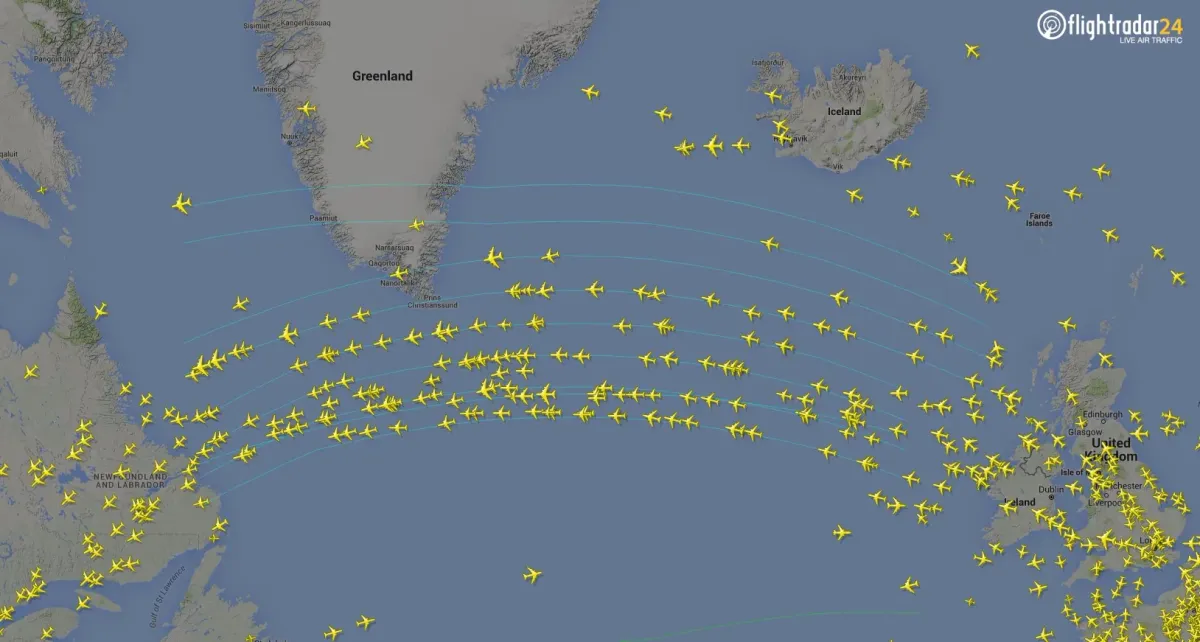
But, what if, say, I wanted to travel from London to New York. Now we are travelling a distance which is significant relative to the curvature of the Earth, and as any seasoned traveller will know, the shortest path is no longer a straight line but a curved route over the North Atlantic and Canada. On such scales, the Earth is no longer a Euclidean surface, so our familiar geometric laws fail.

Let us examine this idea of distance in more detail. On a Euclidean surface, the shortest distance between two points is easy to define using cartesian coordinates and Pythagoras’s law. But what about on the spherical surface of the Earth? Now the shortest path between two points, known formally as a geodesic, is given by the shortest section of the great circle which passes through the two points, where a great circle is a circle who’s centre and radius are the same as of the sphere.

Can we generalise this? Unsurprisingly, the answer is yes. So long as we know how the surface curves — essentially what it looks like — then we can find the geodesics by minimising paths across the surface with respect to their length.

All manifolds can be described by what is known as a metric. This defines how the distance between infinitesimally close points vary across the surface, and in doing so essentially maps out the shape of the surface. For example, if I walk across the short side of the football field, I know that the distance I cover with each step does not depend on how far along the touchline I am. Conversely, if I drive 100 miles due east at the Earth’s equator, my longitude will change a lot less than if I did the same thing in the Arctic circle. This behaviour is encapsulated in the metrics of the two surfaces.

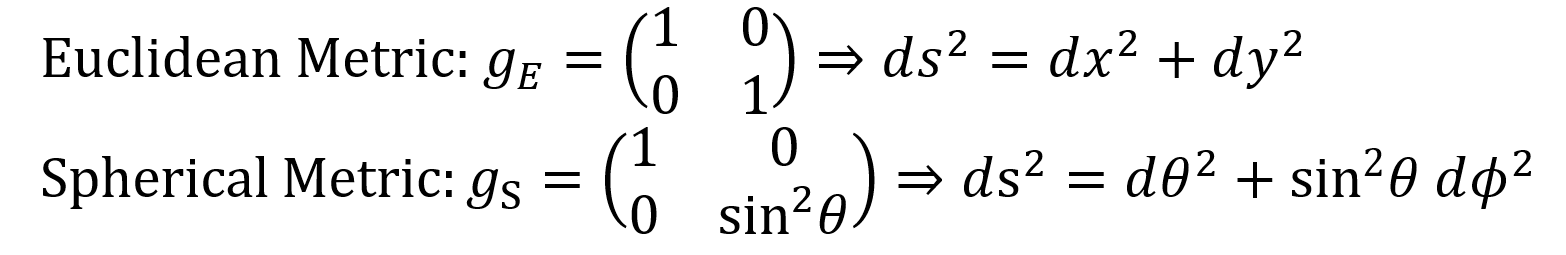
So far, we have only considered 2D surfaces in 3D space, but why stop there? Indeed, a manifold with which you interact with every moment of every day in fact has no fewer than 4 dimensions. I speak, of course, of spacetime.

Until the work of Einstein, the ideas of space and time had been treated as completely independent. It was thought that time ticked away at the same rate for any observer anywhere in the universe, and crucially no matter what speed at which the observer travelled.

Then at the turn of the 20th century, the Michelson-Morely experiment, among others, produced some troubling evidence. Famously, the experiment showed that the speed of light is independent of the motion of the Earth around the sun, which not only disproved the existence of the Lumoniferous aether, but also provided evidence that the speed of light is constant no matter what. This latter conclusion was used by Einstein as a postulate of special relativity and, as a consequence, space and time are intrinsically linked by the theory.

Time is the fourth dimension of our spacetime manifold, along with the familiar three dimensions of space. Our idea of “distance” between two points, or events, on the spacetime manifold must therefore consider time as well as space. Thus, distance in spacetime is encapsulated by the quantity known as the interval. And, just as in the case of 2D surfaces, the form of this interval is entirely determined by the metric of the spacetime.

So, what is the metric of spacetime? As one might expect, it depends. In the simplest case, we have a metric which very closely resembles that of Euclidean space. Such a spacetime is known as Minkowski space, named for the professor of Einstein who first described it in 1908. Such a spacetime is often described as flat, since a Minkowski spacetime treats its 3 spatial coordinates as identical to a 3D Euclidean space. This means all our familiar geometric laws apply, and that the geodesics in Minkowski spacetime are straight lines between events.

Minkowski spacetime arises from the theory of Special relativity. Special relativity, however, only deals with a very specific scenario: one in which all frames of reference — essentially observers — are inertial. This means that special relativity breaks down as soon as something begins to accelerate under the action of a force. If an object accelerates, then its speed changes. Speed is rate of change of distance with time, so if we were to plot an accelerating object’s path through spacetime, known as its worldline, then we would find that it curves. The gradient of its worldline — its speed — is changing over time. But we already know that the geodesics in Minkowski space are straight lines, so an object cannot trace a curved worldline. We have a contradiction! Objects in Minkowski spacetime, and thus under special relativity, cannot accelerate!

But we know that objects do accelerate. Throwing a ball in the air causes it to accelerate, and it accelerates again when it falls back to the ground. So how do we account for this? Thankfully, Einstein once again comes to the rescue with his theory of General Relativity. Under this theory, spacetime is no longer flat. It can curve and flow, even propagate waves under the right circumstances. And, just as the geodesics on a spherical surface are not straight lines, the geodesics in curved spacetime also need not be straight. Under general relativity, objects can once again accelerate.

But why does spacetime curve? One of the critical insights of general relativity is that mass and energy (which are, of course, the same thing in Einstein’s relativity), generate the curvature of spacetime. In the simplest case, that of a spherical body in an otherwise empty — and thus flat — spacetime, the mass of the body curves spacetime into a well.

The geodesics in such a region are curved, and objects encountering the region can follow trajectories ranging from collision courses to stable elliptical orbits and glancing hyperbolic flybys, depending on the speed and direction of the encounter. Sound familiar? This is how objects behave under gravity! Gravity itself is a manifestation of the geodesics of a curved spacetime.

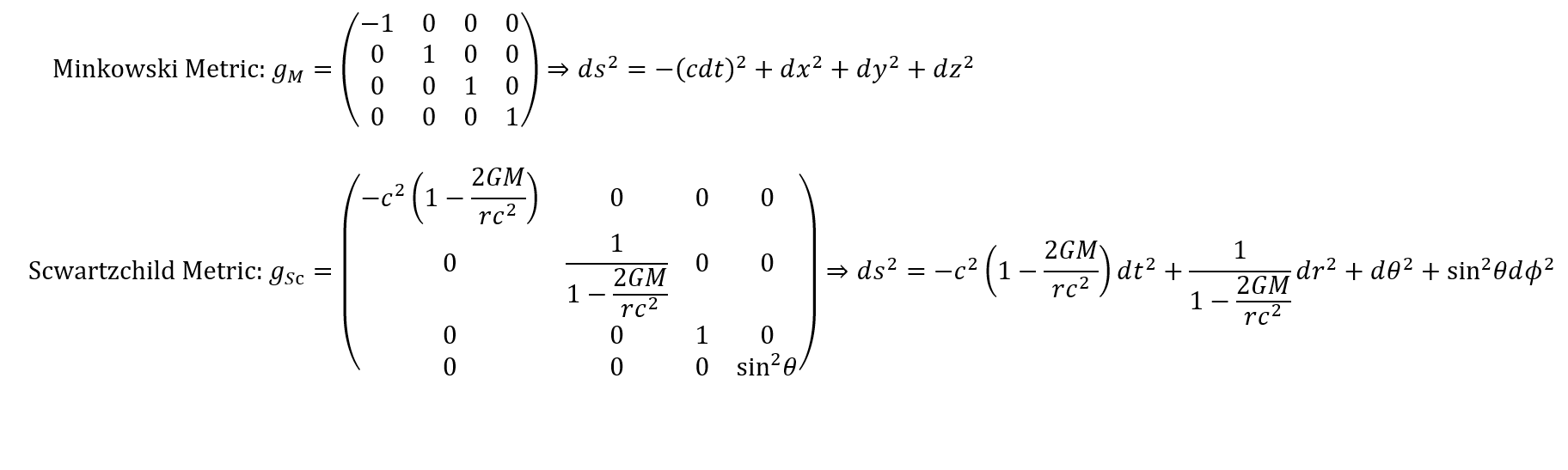
This simplest curved spacetime is described by what is known as the Schwartzchild metric. One of its most famous predictions is the existence of black holes due to singularities in the metric. One of these, at the origin, is a true singularity and its physical manifestation is a subject of debate, but the second at what’s known as the Schwartzchild radius has a well-defined physical meaning. It is the radius of the event horizon of the black hole — the point of no return. Past this point, the curvature of spacetime is so dramatic that speeds greater than that of light are required to escape its grasp, a feat which is impossible under relativity.

Other metrics describing the curvature of spacetime under more complex scenarios exist. Among the best known are the Kerr metric, which describes a charged or rotating black hole, and which, under some extreme circumstances, predicts the existence of traversable wormholes at the heart of such objects. Another is the Freidmann-Lemaître-Robertson-Walker (FLWR) metric, which predicts the expansion rate of the entire universe based on its contents.

Why then, if the very fabric of space and time is constantly warped by our very presence, did it take until the 20th century for anyone to notice? It’s another scale effect! Just as the Earth appears to be flat on our human scales, spacetime itself appears flat when we consider objects as tiny as humans. Even the Earth itself is puny: consider that the escape velocity of the Earth — the speed required to escape the well of spacetime caused by its mass — is just 0.004% of the speed of light. It’s enough that satellites and the moon stay in orbit, but compared to that of a black hole, for example, the curvature of spacetime due to the Earth is barely more than a pimple.

This is why we don’t experience relativistic effects such as time dilation and length contraction on the surface of the Earth. The spacetime surrounding us curves so slowly that it may as well be flat!

And yet, we do occasionally observe the effects of general relativity closer to home than we might expect. The GPS in your phone is a good example. The difference in curvature of spacetime at the geostationary orbits of GPS satellites and the Earth’s surface is sufficient that, if relativistic effects were not accounted for, GPS would be inaccurate by as much as 10 km after only a single day [1].

Whether it’s calculating the flightpath of an aeroplane or the future of the universe, the metric is a powerful tool. It allows for the concise description of a manifold independent of a coordinate system, and as a result the plotting of geodesics through that space. And yet, due to scale effects, the only metric we experience on a day to day basis is that of flat Euclidean space. How very boring indeed!

References

[1] N. Ashby, “Relativity and the Global Positioning System,” Physics Today, no. 41, 2002.