In this article, I want to introduce you to a simple problem with an easy-to-apply, yet awfully unintuitive solution. It is one kind of envelope problem and goes like this

There are two envelopes with some different amounts x and y of money in them. The envelopes look exactly the same and are randomly shuffled before they reach your hands.

Now, you can open one of them and decide whether

• to keep the money that is inside or
• throw away the money that is inside (sorry, that’s the rules 😅), open the other envelope and keep the money inside of this one.

Of course, you try to maximize your reward by picking the best envelope.

That’s it. It’s worth stressing out that you do not know the values of x and y in advance. If you did, the problem of picking the better envelope would be trivial. Also, let us assume that x≠y since otherwise both envelopes are the best and the chance of winning the bigger price is also 100%.

Problem Analysis

So, what to do? We don’t have any information: The letters are shuffled, look the same, and we don’t even know the amount of money that is inside. So there is not really a way to apply some strategy and boost the probability of success beyond 50%, right? Are we dealing with a lost cause?

Of course not.

Otherwise, this article would not exist, duh! There are some easy strategies everyone could come up with:

1. Always stick with the first envelope.
2. Always switch the envelope.

Spoiler: applying one of these two strategies leaves you off with a probability of 50% only of getting the bigger reward. That is because both envelopes were shuffled beforehand, nothing you can do about it.

Let us now cover another strategy that is better suited to increase our success probability.

Increasing the Chances

First, let us assume x<y. Imagine that you know a number z that is between x and y.

In this case, we could apply the following simple strategy:

1. Open an envelope.
2. If the amount inside is smaller than z, choose the other envelope.
3. Otherwise, stick with the initial envelope and call it a day.

Note that this strategy makes us certainly win. So, what’s the catch? We don’t have such a z. We need to adapt. So…

What about if we randomly sample some z and use this?

It sounds crazy but let us go through the calculations and see how this can be any good.

Calculating the Advantage

Let us consider two cases:

1. The first envelope we pick contains x (i.e. the smaller amount).
2. The first envelope we pick contains y (that is what we want).

The case for x first: If we get x first, we have to switch the envelope to end up with y. When does this happen according to our strategy? It happens whenever our randomly sampled z is larger than x. This means that in this case, we win with a probability of P(z>x).

The case for y first: If we get y first, we have to stick with the envelope. This happens whenever our randomly sampled z is smaller than y. This means that in this case, we win with a probability of P(z<y).

Since we land in both of these cases with a probability of 50% (the envelopes were shuffled), we end up with a total success probability of

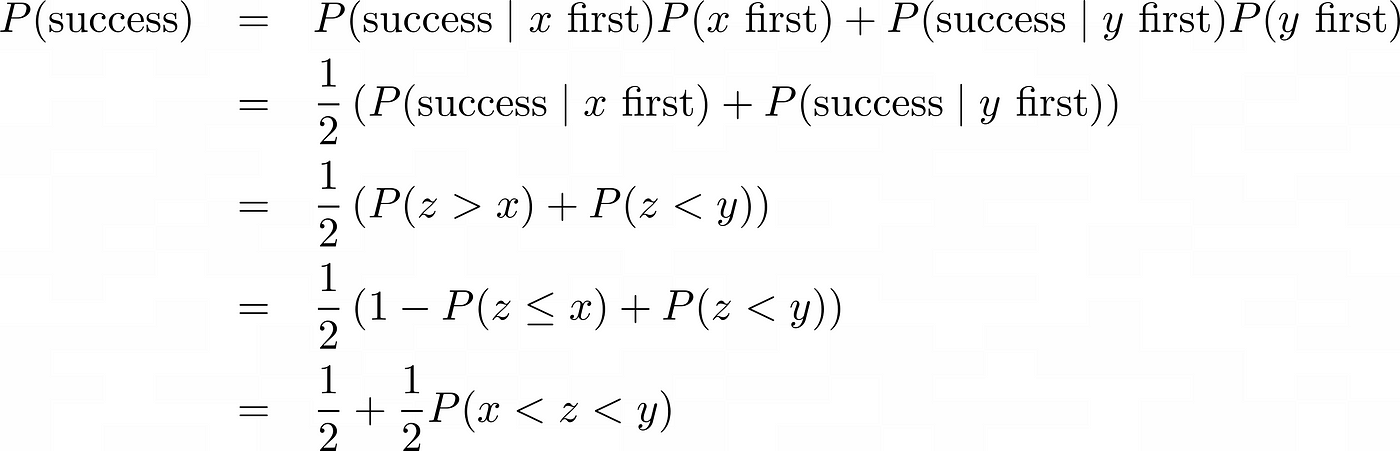
We can see that this probability is at least 50%, and if P(x<z<y)>0, it’s even larger!

The magnitude of this advantage ranges

• from 0% when z is never between x and y
• to 50% when z is always between x and y.

Since we don’t know x and y, we will probably end up somewhere in between. Choosing any distribution that can take on any number makes this advantage definitely strictly greater than zero. Take the normal distribution, for example. For this distribution, we have P(x<z<y)>0, whatever x and y are.

The good thing: The further x and y are apart, the larger the advantage gets!

Incorporating more Knowledge

In our special case, hopefully, x and y are at least positive numbers. Then, we could also use an exponential distribution not waste any probability density on negative numbers.

If you have more knowledge about the magnitudes of x and y, you can use this to narrow down the distribution of z even more!

If you know that both numbers are larger than zero and smaller than a million, for example, you can use the uniform distribution between 0 and 1,000,000.

Conclusion

We have shed light on a special type of envelope problem where we don’t have much data to deal with. Still, we could find a solution that allows us to get the larger reward with a probability that is greater than 50%.

The beauty of this is that you can use this solution for many problems where you don’t have many clues. And it’s an extremely simple solution that people can understand even without knowing mathematics:

You create your own reference point by rolling a die and act according to it.

This is what people naturally do anyway: You have to do a task, but got no instructions on what the goal could be? Well, imagine some reasonable goal, work towards it and see if you achieved it. If not, keep working; otherwise, stop.

I hope that you learned something new, interesting, and useful today. Thanks for reading!