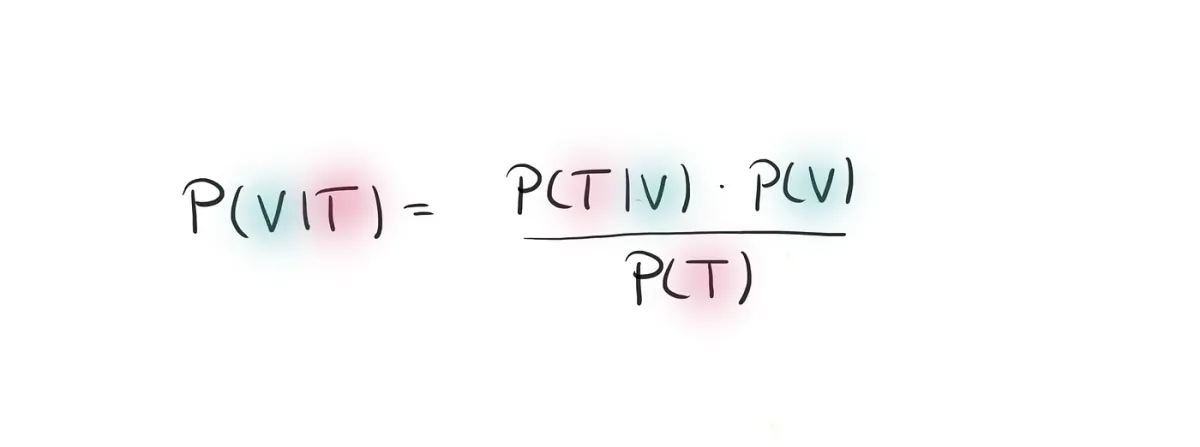
Why more (random) testing doesn’t equal better results

With the current Corona Crisis going on the world, many people demand more testing. But from a mathematical point of view, just randomly (!!) testing more is not the answer. The problem here lies within the false positives that may occur when two very unlikely events are highly correlated.

(Writer’s Note: If you don’t care about the Math, feel free to skip to the bottom. But whatever you conclude from this story, please don’t conclude that the current testing is bullshit. I can assure you — it is not. But a lot of times, people wonder why we don’t just test everybody. Besides the fact, that there are no testing capacities for this, there is also a big (mathematical) reason against that. And that reason will be explained, from a mathematical point of view, in this story.)

Introduction to the Mathematical Problem

A person, let’s call her Sarah, may either have the virus or she doesn’t.

When she takes a test, her results may either come back positive or they come back negative.

In total, there may be four possible situations:

1. Sarah has the virus and she tests positive.

2. Sarah has the virus, but she tests negative.

3. Sarah does not have the virus and she tests negative.

4. Sarah does not have the virus, but she tests positive.

Outcomes 1 and 3 are great in terms of a correct test. Outcome 2 is bad for society (Sarah will think she doesn’t have the virus, but may walk around passing it on to others) and outcome 4 sucks for Sarah (she’s gonna have to stay home alone to quarantine even though she’s totally fine), but better for society.

Most medical tests are between 90–99 % correct. Correct is not the best term to use, as “correct” means two things:

1. 99 % correct means that out of 100 people who have the virus, 99 of them will get a positive test result. This is called sensitivity. In mathematical terms, sensitivity is the conditional probability of ‘T’ given ‘V’.
2. 99 % correct also means that of 100 people who do not have the virus, 99 of them will get a negative result. This is called specificity. In mathematical terms, specificity is the conditional probability of ‘not T’ given ‘not V’.

Always remember that sensitivity and specificity do NOT need to be the same number!

There are many reasons why tests may be incorrect. Some say because sometimes the virus load is too low or the samples taken are not clean enough. There are various reasons. I’m not a doctor, so I’m not gonna go into details here.

Sensitivity and specificity are great, except that by themselves, they are not very useful. After all, if we already knew who had the virus and who didn’t, what would be the point of testing?

This is where Math comes into play and more specifically, Bayes’ Theorem.

Bayes’ Theorem: Why and What

What we are really interested in is the probability of somebody being infected with the virus after getting back a positive test result (instead of the probability of a correct test given that somebody is sick).

Mathematically speaking, this is the probability of V given T.

And to calculate this, we can use Bayes’ Theorem, which is given by

Bayes’ Theorem basically flips around the condition. Before we were conditioning on infected people, now we condition on positively tested people.

That means that instead of looking at all the people who have the virus (we don’t know who they are — if we did, a lot of our problems would be solved), we look at all the people who were positively tested. Since these people signed up for a test, it should be fairly easy to find them.

We still need the probability of being tested positive.

The probability of being tested positive is composed of the events of being both positively tested and actually infected as well as being positively tested without being infected.

To get the latter two probabilities, we can rewrite the definitions of the conditional probability. For sensitivity, this leads to

and for specificity, this leads to

Thus, the probability of being positively tested is given by

We can now put everything together in the Theorem of Bayes and get a formula that appears to be a bit blown out of proportion, but is in fact correct:

This formula only depends on sensitivity (blueish), specificity (reddish), and the overall infection rate P(V).

Punching in Numbers

Now comes the interesting part: Punchin in numbers! To make it easy, here’s a tiny Python scribble that you can just copy and paste to a Jupyter Notebook to play around for a bit.

spec = 0.99
sens = 0.99
infected = 0.001
VgivenT = (sens*infected)/(sens * infected + (1- spec)*(1-infected))
print(VgivenT)

this is where it gets interesting. The above code with a sensitivity and specificity of around 99 % and an infection rate of roughly 0.1 % (i.e. 1 in every 1000 persons is, in fact, infected) gives us a probability of less than 10% that somebody who gets tested positive actually has corona!

If the amount of infected people is 1%, then this probability increases to roughly 50% and if the amount of infected people is 50%, it increases to 99% (i.e. the value of the sensitivity and specificity).

Surprisingly low, isn’t it?

Conditional probabilities usually return unintuitive results whenever we have two different events (V, T) that are highly correlated but where one of them has a very small probability.

The Intuitive Explanation

There is a very intuitive explanation. Let’s assume that the actual infection rate is 0.1 %. In the USA, there are approximately 330 million people. If 0.1 % are infected, there are 330,000 infected people out there and 329,667,000 non-infected people. Of these non-infected people, 1% should get a false positive. That is 3296700 people and roughly 10 times more than people who are actually infected!

If, however, there are 1 % infected people, i.e. 3,300,000 infected people, then there are also 326,700,000 non-infected people of which 3,267,000 should get a false-positive test result, which is roughly the same number as actually infected people.

This ratio shrinks as the infection rate goes up.

Conclusion

That’s why, whenever you have a positive test result, but little to no symptoms, it makes sense to get tested again to double-check your results. The chances of (falsely) getting more than one positive result in a row are very very very small. So if you get two or more positive results in a row, you can be sure to have caught the virus.

Also, it is the reason, why it doesn’t make sense to just randomly go out and test everybody. Besides the fact that there aren’t enough testing capacities for this, we would get so many false positives that the results wouldn’t be very useful.

But, and this is a big but: I have been lying to you this whole story. The infection rate we have been using should not be used like this. And the Math doesn’t apply like this to the real-world.

Because this Math only applies where being tested is independent of being infected and that is not the case in the real-world!

I repeat: Testing and actual infections are not independent!

But, scientists know this. And that is one of the reasons why they don’t just go out and test every single person out there. Instead, they test people who either have symptoms or who were in close contact with an infected person. Mathematically speaking: People who have a much higher probability of being infected than the overall infection rate in a country. By doing this, we actually keep the false positives rate fairly low and much closer to the 1% error rate advertised.

Because mathematically, this strategy leads to a similar result as an increased infection rate: The relative number of false positives decreases as the selection of people tested becomes smarter.

To conclude: No, I don’t believe that we have millions of false positives out there. I think all of the deaths we are witnessing are proof enough. This story is not meant to discredit any of the testings.

In fact, the testing that is currently done is probably a lot smarter than most people think it is. Because there is a big reason (backed up by Math! And explained in this story), why it makes sense to only test when there is a plausible reason to believe that somebody might have contracted the virus.

It makes the most sense to test when there is a plausible reason to believe that somebody might have contracted the virus, either by having been in close contact with an infected person or because they have strong symptoms.

This story is supposed to be a reminder of why more testing does not always mean better results. And an even stronger reminder that statistics are not always that simple. Because statistics can very easily be misinterpreted and by the very nature of them, statistics contain many errors.

I have been studying Math and Statistics for almost a decade now, pondering about it every day. And the one thing I am certain about is:

Nothing is certain in statistics.