Relativity

A Gentle Explanation of E= mc²

Deriving Einstein’s Famous Mass-Energy Equivalence Formula

Marco Tavora

15 Dec 2020 — 6 min read

The mass-energy equivalence formula E = mc² defines a relationship between the mass m and the energy E of a body in its rest frame (the rest frame is the frame of reference where the body is at rest). The square of the speed of light is an enormous number, and therefore a small amount of rest mass is associated with a tremendous amount of energy.

Figure 1: In the blackboard, a variant (*Eq. 9 of this article) of his famous equation, E = mc*² (source).

The Annus Mirabilis papers

While still working as a patent clerk, Einstein published four revolutionary papers, all of them containing major contributions to the foundations of modern physics:

In the first paper, he explained the so-called photoelectric effect, the emission of electrons when light hits an object. He also showed that energy consists of discrete packets (photons).

Figure 2: Electrons are emitted from a metal plate due to light quanta (photons) (source).

The second paper explained Brownian motion, the random motion of particles suspended in a medium. This paper led the physics community to accept the atomic hypothesis.

Figure 3: Simulation of the Brownian motion of 5 particles (yellow) colliding with 800 particles. The particles leave blue trails (from their random motion) (source).

In the third paper, Einstein introduced his theory of special relativity. For a very quick introduction to some of the features of special relativity see two of my recent articles:

Why Clocks in Motion Slow Down According to Relativity Theory

In the fourth paper, Does the Inertia of a Body Depend Upon Its Energy Content? (Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?), which will be the focus of the present article, Einstein developed the principle of mass-energy equivalence E = mc² (leading eventually to the discovery of atomic energy).

Figure 4: The front page of the paper “*Does the Inertia of a Body Depend Upon Its Energy Content?”* where Einstein developed the principle of mass-energy equivalence principle E = mc² (source).

The Postulates of Special Relativity

Let us quickly recall the two postulates of special relativity:

All the laws of physics are the same in all inertial reference frames.
The speed of light in a vacuum is the same in all inertial reference framesregardless of the motion of the observer or the source.

Redefining Momentum

This section will show that the classical (nonrelativistic) linear momentum p=mv, which has a corresponding conservation law in classical mechanics, must be redefined for the momentum conservation to continue valid in relativistic regimes.

A Bird’s Eye View of Lorentz Transformations

If in an inertial system S the coordinates of an event E are given by (t, x, y, z), in a moving frame S’ with constant velocity v with respect to the first inertial system, the same event E will have coordinates (t’, x’, y’, z’) given by:

Figure 5: Two inertial frames moving with velocity v with respect to each other (source).

These relations are called Lorentz transformations (named after the Dutch physicist Hendrik Lorentz).

Minkowski Diagrams

The spacetime in special relativity is represented graphically by Minkowski diagrams, two- or three-dimensional graphs with one or two space dimensions and one time dimension (see Fig. 7).

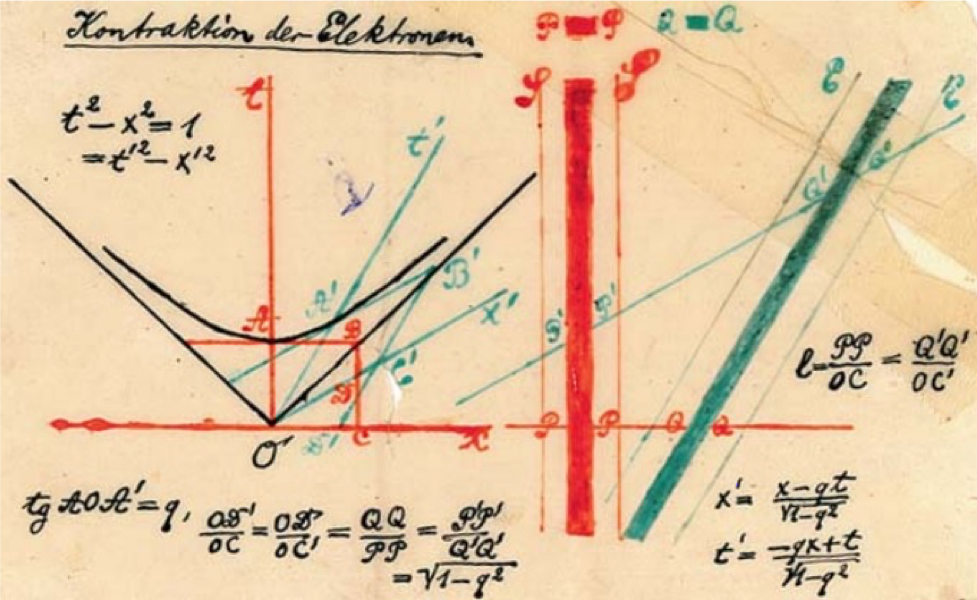
Figure 6: A transparency from Minkowski’s famous talk, “Space and Time” (1908) (source).

Two important concepts are represented in a Minkowski diagram:

Events: An event is an instantaneous occurrence, represented by a point (t, x, y).
World line: a line representing the motion of an object through time. The slope of the world line is the reciprocal of the velocity of the moving object (since by convention the time axis is the vertical one).

Figure 7: The Minkowski diagram where the worldline represents the motion of an object through time. The slope of the world line is, by convention, the reciprocal of the velocity of the moving object (source).

Proper Time and Proper Velocity

Proper time τ is the time your clock registers as you move, say, inside a plane. More specifically, it is the time measured by a clock following a world line in spacetime. It is related to the external time (say, the time measured by a clock on the ground) by the following relation:

Equation 2: Relation between proper time (the time *your* clock registers as *you* move) and the time measured by a clock on the wall.

The proper velocity η = dl/dτ is defined using the external distance and the propertime. Since dl/dτ = dl/dt × dt/dτ = v × dt/dτ, Eq. 2 above gives us:

Equation 3: Definition of proper velocity.

For example, if you are on a plane, η measures the ratio between the distance it takes for the plane to complete the trip (measured by an observer on the ground) and the time aboard the plane (registered on your watch).

Eq. 3 is the spatial part of the proper velocity. The 0-th component is:

Equation 4: The 0-th component of the proper velocity

Relativistic Momentum

In nonrelativistic (or classical) mechanics, the momentum is equal to the (constant) mass times the velocity p = mv. However, in the relativistic domain, the law of conservation of classical momentum violates the principle of relativity (it is straightforward to find a pair of reference frames S and S’ where the total momentum is conserved in S and not in S’ or vice-versa).

To recover the validity of the principle of relativity, we must redefine the momentum’s expression. This turns out to be fairly easy: we simply use the relativistic momentum below instead of the classical momentum:

Equation 5: Definition of relativistic momentum.

Rest Energy

The 0-th component of Eq. 5 is given by

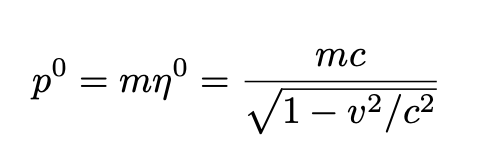
In his 1905–1906 papers, Einstein called relativistic mass the quantity:

Equation 6: Einstein’s definition of relativistic mass.

and m he called rest mass. Nowadays, the terminology has changed and relativistic energy is defined by:

*Equation 7: Relativistic energy (modern definition).*

Now, notice that even if the object is not moving (v=0), it still has nonzero relativistic energy. This is the rest energy of the object:

To obtain the kinetic energy we subtract the rest energy from the total energy:

Thanks for reading and see you soon! As always, constructive criticism and feedback are always welcome!

My Linkedin posts, my personal website www.marcotavora.me, and my Githubprofile have some other interesting content about physics and other topics such as mathematics, machine learning, deep learning, finance, and much more! Check them out!